12 ANOVA à critères multiples : plans factoriels et hiérarchiques

Objectifs de ce chapitre :

Utiliser R pour faire une ANOVA paramétrique d’un plan factoriel avec deux facteurs de classification et réplication
Utiliser R pour faire une ANOVA paramétrique d’un plan factoriel avec deux facteurs de classification sans réplication
Utiliser R pour faire une ANOVA paramétrique d’un plan hiérarchique avec réplication
Utiliser R pour faire une ANOVA non paramétrique avec deux facteurs de classification
Utiliser R pour faire des comparaisons multiples

Il existe une très grande variété de plans (designs) d’ANOVA que R peut analyser. Cet exercice n’est qu’une introduction aux plans les plus communs.

12.1 Paquets et données requises pour le labo

Pour ce laboratoire, vous aurez besoin de :

Paquets R :
- multicomp 📦
- car 📦
- tidyverse 📦
Jeux de données :
- “Stu2wdat.csv”
- “Stu2mdat.csv”
- “nr2wdat.csv”
- “nestdat.csv”
- “wmcdat2.csv”
- “wmc2dat2.csv”

library(multcomp)
library(car)
library(tidyverse)

12.2 Plan factoriel à deux facteurs de classification et réplication

Il est fréquent de vouloir analyser l’effet de plusieurs facteurs simultanément. L’ANOVA factorielle à deux critères de classification permet d’examiner deux facteurs à la fois, mais la même approche peut être utilisée pour 3, 4 ou même 5 facteurs quoique l’interprétation des résultats devienne beaucoup plus complexe.

Supposons que vous êtes intéressés par l’effet de deux facteurs : le site (location, Cumberland House ou The Pas) et le sexe (sex, mâle ou femelle) sur la taille des esturgeons. Comme l’effectif n’est pas le même pour tous les groupes, c’est un plan qui n’est pas balancé. Notez aussi qu’il y a des valeurs manquantes pour certaines variables, ce qui veut dire que chaque mesure n’a pas été effectuée sur chaque poisson.

12.2.1 ANOVA à effets fixes (Modèle I)

Examinez d’abord les données avec des “boxplots” de la taille (rdwght) selon le sex et la location des données du fichier Stu2wdat.csv .

Solution

Stu2wdat <- read.csv("data/Stu2wdat.csv")

ggplot(Stu2wdat, aes(x = sex, y = rdwght)) +
geom_boxplot(notch = TRUE) +
facet_grid(~location)

Warning: Removed 4 rows containing non-finite outside the scale range
(`stat_boxplot()`).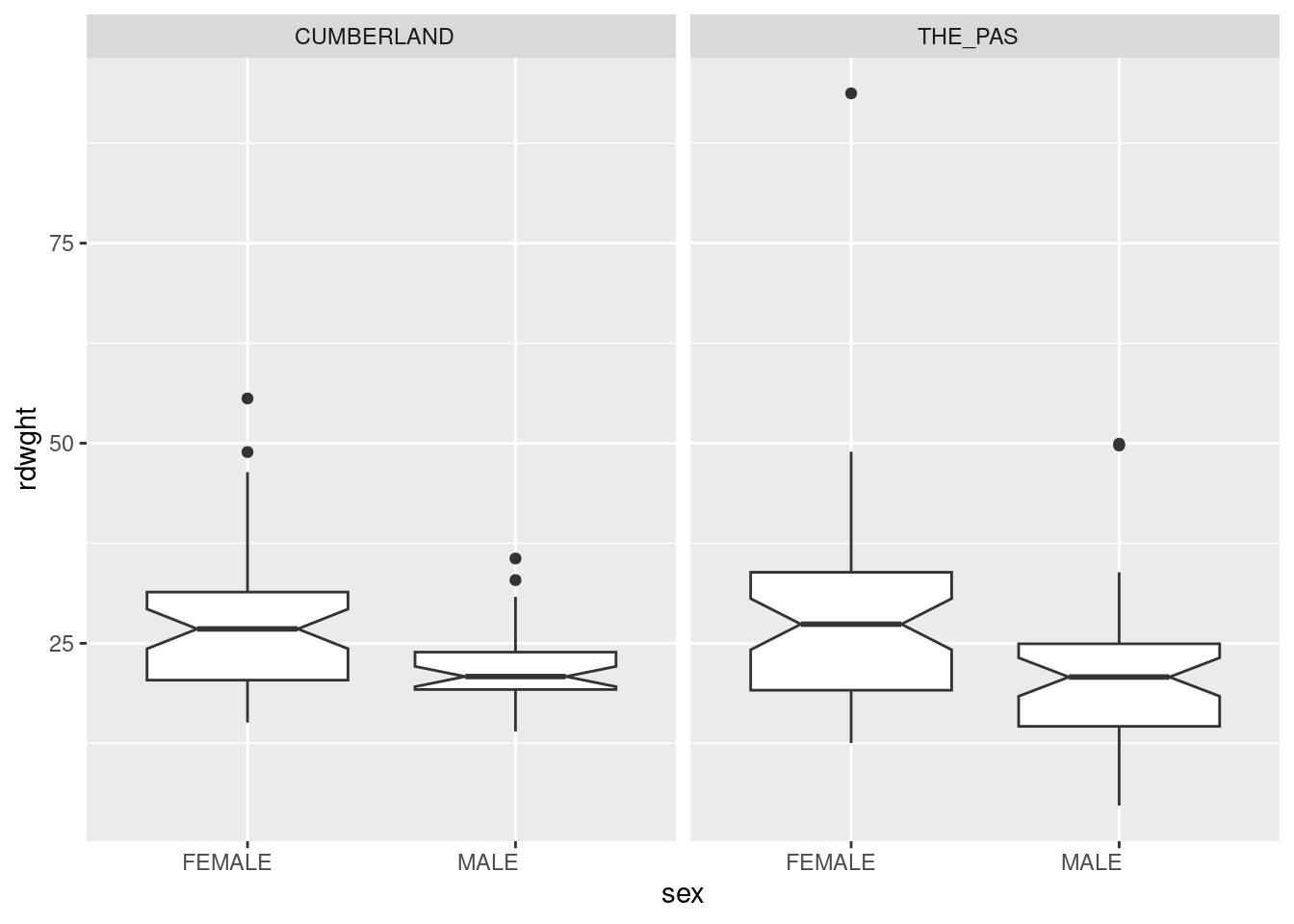

Les graphiques montrent qu’aux deux sites les femelles sont probablement plus grandes que les mâles, mais que les tailles ne varient pas beaucoup d’un site à l’autre. La présence de valeurs extrêmes sur ces graphiques suggère qu’il y aura peut-être des problèmes avec la condition de normalité des résidus.

Résumez les statistiques de taille (rdwght) selon le sex et la location.

Moyenne, écart-type, taille d’échantillon

Stu2wdat %>%
  group_by(sex, location) %>%
  summarise(
    mean = mean(rdwght, na.rm = TRUE), sd = sd(rdwght, na.rm = TRUE), n = n()
  )

`summarise()` has grouped output by 'sex'. You can override using the `.groups`
argument.

# A tibble: 4 × 5
# Groups:   sex [2]
  sex            location        mean    sd     n
  <chr>          <chr>          <dbl> <dbl> <int>
1 "FEMALE      " "CUMBERLAND  "  27.4  9.33    51
2 "FEMALE      " "THE_PAS     "  28.0 12.5     55
3 "MALE        " "CUMBERLAND  "  22.1  4.79    34
4 "MALE        " "THE_PAS     "  20.6  9.92    46

Ces résultats supportent l’interprétation des “boxplots” : Les femelles sont plus grosses que les mâles, et la différence de taille entre les deux sites n’est pas énorme.

Faites une ANOVA factorielle à deux critères de classification avec les données de Stu2wdat.csv :

# Ajuster un modèle (ANOVA) et faites le graphiques des résidues
# Mais d'abord, sauvegardez les paramètres graphiques actuels
opar <- par()
anova.model1 <- lm(rdwght ~ sex + location + sex:location,
  contrasts = list(sex = contr.sum, location = contr.sum),
  data = Stu2wdat
)
anova(anova.model1)

Analysis of Variance Table

Response: rdwght
              Df  Sum Sq Mean Sq F value    Pr(>F)    
sex            1  1839.6 1839.55 18.6785 2.569e-05 ***
location       1     4.3    4.26  0.0433    0.8355    
sex:location   1    48.7   48.69  0.4944    0.4829    
Residuals    178 17530.4   98.49                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Avertissement

Attention, R imprime les sommes des carrés séquentielles (Type I) les carrés moyens et probabilités associés. Vous ne pouvez pas vous y fier si votre plan d’expérience n’est pas parfaitement balancé. Dans cet exemple, le nombre de poissons capturés change selon le site et le sexe et le plan d’expérience n’est donc pas balancé.

Vous devez extraire les sommes de carrés partielles (Type III). Le moyen le plus simple est d’utiliser la fonction Anova() du paquet car 📦 (notez une différence subtile mais fondamentale, Anova() n’est pas la même chose que anova(), R est impitoyable et distingue les majuscules des minuscules). Malheureusement, ça ne suffit pas. Il faut également spécifier le type de contraste dans le modèle avec l’argument

contrasts = list(sex = contr.sum,location = contr.sum)

library(car)
Anova(anova.model1, type = 3)

Anova Table (Type III tests)

Response: rdwght
             Sum Sq  Df   F value    Pr(>F)    
(Intercept)  106507   1 1081.4552 < 2.2e-16 ***
sex            1745   1   17.7220 4.051e-05 ***
location          9   1    0.0891    0.7656    
sex:location     49   1    0.4944    0.4829    
Residuals     17530 178                        
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Suite à l’ANOVA, on accepte deux hypothèses nulles:

L’effet du sexe ne varie pas entre les sites (pas d’interaction significative)
Il n’y a pas de différence de taille des esturgeons (peu importe le sexe) entre les deux sites.

D’un autre coté, on rejette l’hypothèse nulle qu’il n’y a pas de différence de taille entre les esturgeons mâles et les femelles, tel que suggéré par les graphiques.

par(mfrow = c(2, 2))
plot(anova.model1)

Figure 12.2: Conditions d’application ANOVA model1

Mais ! Comme d’habitude, on ne peut pas accepter les résultats sans d’abord nous assurer que les conditions d’applications sont respectées.

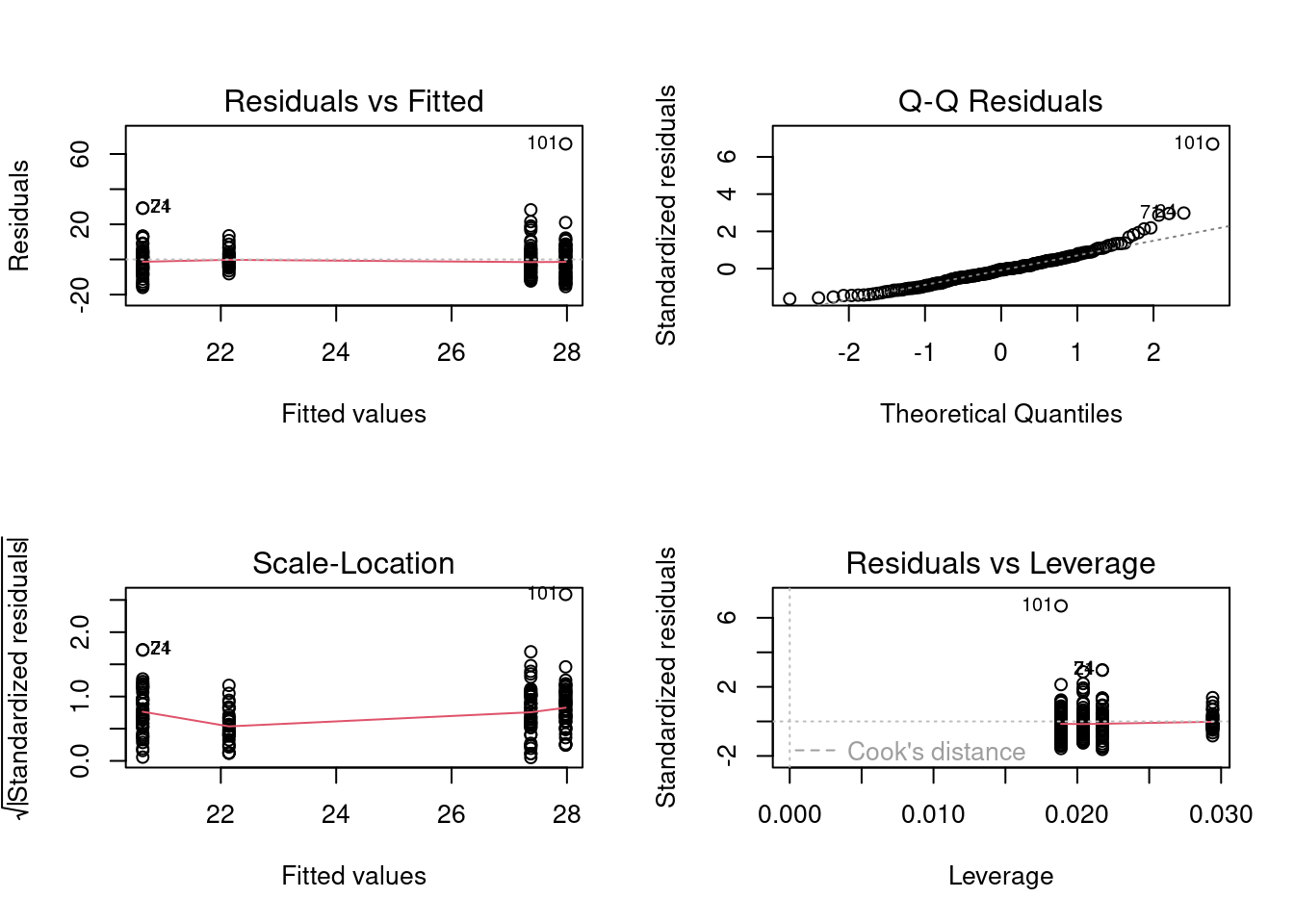
Normalité : L’examen des graphiques des résidus ci-dessus montre que l’écart à la normalité reste raisonnable, avec seulement 3 potentielles valeurs abérrantes sur le graphique QQ (cas 101, 24 & 71). Cependant leurs distances de Cook ne sont pas importantes (On ne voit même pas la borne 0.5 sur le graphique), il y a donc peu d’indication que ces valeurs sont préoccupantes pour le suite. Si on test la normalité, on obtient:

shapiro.test(residuals(anova.model1))


    Shapiro-Wilk normality test

data:  residuals(anova.model1)
W = 0.87213, p-value = 2.619e-11

Il y a évidence que les résidus ne sont pas distribués normalement (p < 0.05).

Homoscédasticité : Le graphique des résidus par rapport à l’ajustmeent montre que la dispersion des résidus est à peu près égales pour l’ensemble des valeurs ajustés (à l’exception de quelques cas encore un fois). Nous utilisons le test de Levene pour tester cela (de la même façon qu’on a fait pour l’ANOVA à un critère de classification).

library(car)
leveneTest(rdwght ~ sex * location, data = Stu2wdat)

Levene's Test for Homogeneity of Variance (center = median)
       Df F value  Pr(>F)  
group   3  3.8526 0.01055 *
      178                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Si les résidus étaient homoscédastiques, on accepterait l’hypothèse nulle que la moyenne des valeurs absolues des résidus ne varie pas entre les sexes et les sites (i.e., sex:location). Le tableau d’ANOVA ci-dessus montre que l’hypothèse est rejetée. Il y a donc hétéroscédasticité.

En bref, nous avons plusieurs conditions d’application non respectées. La question qui reste est : ces violations sont-elles suffisantes pour invalider nos conclusions ?

Exercice

Répétez la même analyse avec les données du fichier stu2mdat.csv . Que concluez-vous? Supposons que vous vouliez comparer la taille des mâles et des femelles. Comment cette comparaison diffère entre les deux jeux de données ?

Solution

Stu2mdat <- read.csv("data/Stu2mdat.csv")
anova.model2 <- lm(
  formula = rdwght ~ sex + location + sex:location,
  contrasts = list(sex = contr.sum, location = contr.sum),
  data = Stu2mdat
)
summary(anova.model2)
Anova(anova.model2, type = 3)


Call:
lm(formula = rdwght ~ sex + location + sex:location, data = Stu2mdat, 
    contrasts = list(sex = contr.sum, location = contr.sum))

Residuals:
    Min      1Q  Median      3Q     Max 
-15.917  -6.017  -0.580   4.445  65.743 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)     24.5346     0.7461  32.885  < 2e-16 ***
sex1            -0.5246     0.7461  -0.703    0.483    
location1        0.2227     0.7461   0.299    0.766    
sex1:location1   3.1407     0.7461   4.210 4.05e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.924 on 178 degrees of freedom
  (4 observations deleted due to missingness)
Multiple R-squared:  0.09744,   Adjusted R-squared:  0.08223 
F-statistic: 6.405 on 3 and 178 DF,  p-value: 0.0003817

Notez que cette fois les femelles sont plus grandes que les mâles à Cumberland House, mais que c’est le contraire à The Pas. Quel est le résultat de l’ANOVA (n’oubliez pas qu’il faut des sommes des carrés de Type III pour les résultats) ?

Anova Table (Type III tests)

Response: rdwght
             Sum Sq  Df   F value    Pr(>F)    
(Intercept)  106507   1 1081.4552 < 2.2e-16 ***
sex              49   1    0.4944    0.4829    
location          9   1    0.0891    0.7656    
sex:location   1745   1   17.7220 4.051e-05 ***
Residuals     17530 178                        
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

L’interaction (sex:location) est maintenant significative mais les effets principaux ne le sont pas.

Il est utile ici de créer des graphiques pour les deux jeux de données pour comparer les interactions entre sex et location. Le graphique d’interaction montre les relations entre les moyennes de chaque combinaison de facteurs (appelées aussi les moyennes des cellules).

Générez un graphique illustrant les intéractions en utilisant la fonction allEffects() du paquet effects 📦 :

library(effects)
allEffects(anova.model1)

 model: rdwght ~ sex + location + sex:location

 sex*location effect
              location
sex            CUMBERLAND   THE_PAS     
  FEMALE           27.37347     27.97717
  MALE             22.14118     20.64652

plot(allEffects(anova.model1), "sex:location")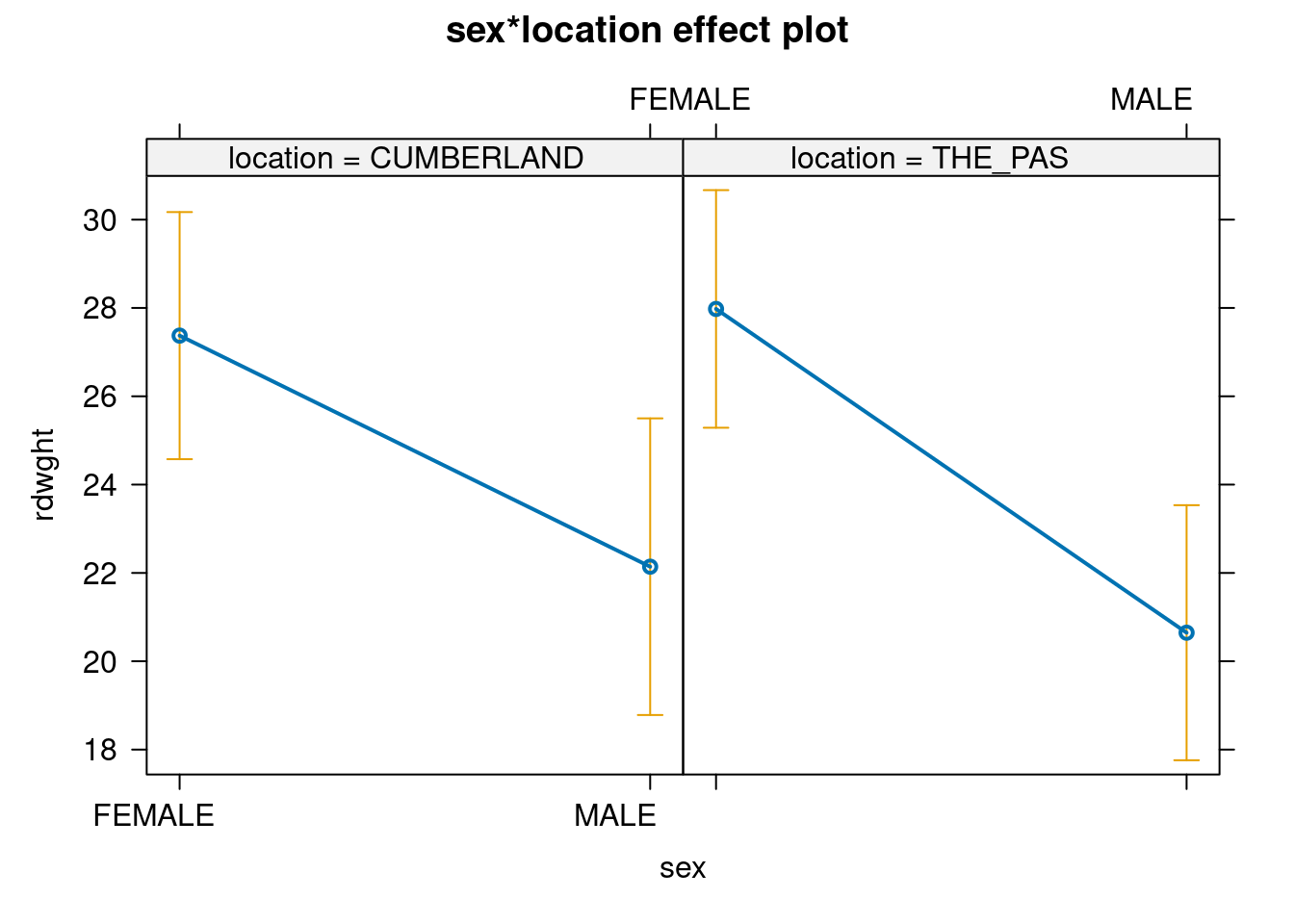

Figure 12.3: Effet du sexe et du lieu sur le poids des esturgeons (1er modèle)

allEffects(anova.model2)

 model: rdwght ~ sex + location + sex:location

 sex*location effect
              location
sex            CUMBERLAND   THE_PAS     
  FEMALE           27.37347     20.64652
  MALE             22.14118     27.97717

plot(allEffects(anova.model2), "sex:location")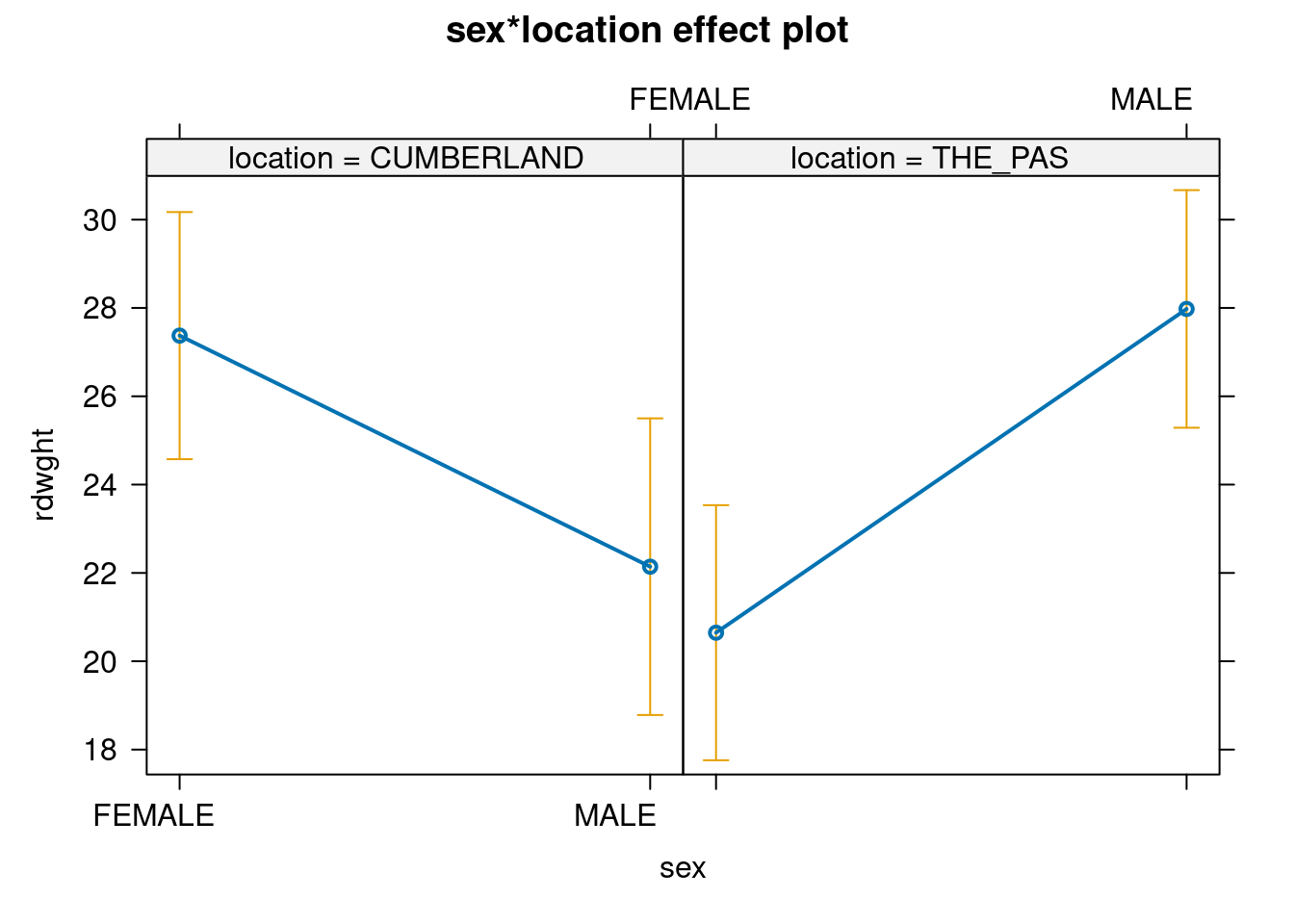

Figure 12.4: Effet du sexe et du lieu sur le poids des esturgeons (2e modèle)

Il y a une différence importante entre les résultats obtenus avec stu2wdat et stu2mdat. Dans le premier cas, puisqu’il n’y a pas d’interaction, on peut regrouper les données des deux niveaux d’un facteur (le site, par exemple) pour éprouver l’hypothèse d’un effet de l’autre facteur (le sexe).

En fait, si on fait cela et que l’on calcule une ANOVA à un critère de classification (sex), on obtient:

Anova(aov(rdwght ~ sex, data = Stu2wdat), type = 3)

Anova Table (Type III tests)

Response: rdwght
            Sum Sq  Df F value    Pr(>F)    
(Intercept)  78191   1 800.440 < 2.2e-16 ***
sex           1840   1  18.831 2.377e-05 ***
Residuals    17583 180                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Notez que la somme des carrés des résidus (17,583) est presque égale à celle du modèle complet (17,530) de l’ANOVA factorielle à deux facteurs. C’est parce que dans cette anova factorielle, le terme d’interaction et le terme représentant l’effet du site n’expliquent qu’une partie infime de la variabilité.

D’un autre coté, si on essaie le même truc avec stu2mdat, on obtient:

Anova(aov(rdwght ~ sex, data = Stu2mdat), type = 3)

Anova Table (Type III tests)

Response: rdwght
            Sum Sq  Df  F value Pr(>F)    
(Intercept)  55251   1 515.0435 <2e-16 ***
sex            113   1   1.0571 0.3053    
Residuals    19309 180                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ici la somme des carrées des résidus (19,309) est beaucoup plus grande que celle de l’ANOVA factorielle (17,530) parce qu’une partie importante de la variabilité expliquée par le modèle est associée à l’interaction.

Notez que si on n’avait fait que cette analyse, on conclurait que les esturgeons mâles et femelles ont la même taille. Et pourtant, leur taille diffère : seulement la différence est à l’avantage des mâles à un site et à l’avantage des femelles à l’autre. Il est donc délicat d’interpréter l’effet principal (sexe) en présence d’une interaction significative !

12.2.2 ANOVA à effets mixtes (Modèle III)

Les analyses qui précèdent négligent un point important, lié au type de modèle ANOVA que l’on veut faire tourner.

Dans cet exemple, le site (location) pourrait être traité comme un facteur aléatoire et le sexe (sex) comme un effet fixe. Par conséquent le modèle approprié d’ANOVA est un modèle mixte.

Notez que dans toutes les analyses qui précèdent, R a traité tous les termes de cette ANOVA comme des effets fixes , et les termes principaux et d’interaction ont été testés en utilisant le carré moyen des résidus comme dénominateur des tests de F.

Cependant, pour une ANOVA mixte, ces effets devraient être testés en utilisant le carré moyen du terme d’interaction, ou en combinant la somme des carrés de l’erreur et de l’interaction (selon le statisticien consulté!).

En utilisant Stu2wdat, refaites un tableau d’ANOVA pour rdwght en considérant le site (location) comme facteur aléatoire et le sexe (sex) comme un facteur fixe.

Pour ce faire, vous devrez recalculer les valeurs de F pour sex et location en utilisant le carré moyen de l’interaction sex:location au lieu du carré moyen des résidus comme dénominateur.

Le mieux c’est de le faire à la main travaillant avec les sommes des carrés d’ANOVA de Type III.

Solution

Anova(anova.model1, type = 3)

Anova Table (Type III tests)

Response: rdwght
             Sum Sq  Df   F value    Pr(>F)    
(Intercept)  106507   1 1081.4552 < 2.2e-16 ***
sex            1745   1   17.7220 4.051e-05 ***
location          9   1    0.0891    0.7656    
sex:location     49   1    0.4944    0.4829    
Residuals     17530 178                        
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pour sex, la nouvelle valeur de F (le rapport des carrés moyens) est de

\[F = \frac{(1745/1)}{(49/1)} = 35.6\]

Pour obtenir la valeur de p correspondant à cette statistique F, on utilise la fonction de probabilité de la distribtuion de F :

pf(F, df1, df2, lower.tail = FALSE),

où F est la valeur de F calculée, et df1 et df2 sont les degrés de liberté du numérateur (sex) et dénominateur(sex:location).

pf(35.6, 1, 1, lower.tail = FALSE)

[1] 0.1057152

Notez que maintenant la valeur de p pour sex n’est plus significative.

C’est parce que le carré moyen de l’erreur dans l’ANOVA initiale est plus petit que celui associé à l’interaction, mais surtout parce que le nombre de degrés de liberté pour le dénominateur du test de F est passé de 178 à 1 seulement.

En général, c’est beaucoup plus difficile d’obtenir des résultats significatifs quand les degrés de liberté pour le dénominateur sont petits.

Note

Les modèles mixtes qui sont une généralisation de l’ANOVA à effets mixtes sont maintenant extrêmement bien développé et sont à favoriser lors d’analyse incluant des effets dit aléatoires.

12.3 Plan factoriel à 2 facteurs de classification sans réplication

Dans certains plans d’expérience il n’y a pas de réplicats pour chaque combinaison de facteurs, par exemple parce qu’il serait trop coûteux de faire plus d’une observation. L’ANOVA à deux critères de classification est quand même possible dans ces circonstances, mais il y a une limitation importante.

Avertissement

Étant donnée qu’il n’y a pas de réplication, on ne peut pas estimer la variance du terme d’erreur : on a simplement la somme des carrées des lignes, une somme des carrés des colones et une somme des carré restants. Cela a des implications importantes :

S’il y a une interaction dans un ANOVA de modèle III, seul l’effet fixe peut être testé (sur la somme des carrés restants) ; pour les ANOVA de modèle I, ou pour les effets aléatoires dans les ANOVA de modèle III, il n’est pas approprié de tester les effets principaux sur le reste, à moins d’être sur de l’absence d’interaction.

Un limnologiste qui étudie Round Lake dans le Parc Algonquin prend une seule mesure de température (temp, °C) à 10 profondeurs différentes (depth, m) à quatre dates (date) au cours de l’été. Ses données sont dans le fichier nr2wdat.csv.

Effectuez une ANOVA à 2 critères de classification en utilisant temp comme variable dépendante et date et depth comme variables indépendantes (vous devez changer le type de données pour depht pour que R traite cette variable comme un facteur et non pas une variable continue).

nr2wdat <- read.csv("data/nr2wdat.csv")
nr2wdat$depth <- as.factor(nr2wdat$depth)
anova.model4 <- lm(temp ~ date + depth, data = nr2wdat)
Anova(anova.model4, type = 3)

Anova Table (Type III tests)

Response: temp
             Sum Sq Df  F value    Pr(>F)    
(Intercept) 1511.99  1 125.5652 1.170e-11 ***
date         591.15  3  16.3641 2.935e-06 ***
depth       1082.82  9   9.9916 1.450e-06 ***
Residuals    325.12 27                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Si on suppose que c’est un modèle d’ANOVA mixte (date aléatoire, depth fixe), que concluez vous ?

Indice: faites un graphique d’interaction de la température en fonction de la profondeur et de la date, pour voir ce qui se passe.

interaction.plot(nr2wdat$depth, nr2wdat$date, nr2wdat$temp)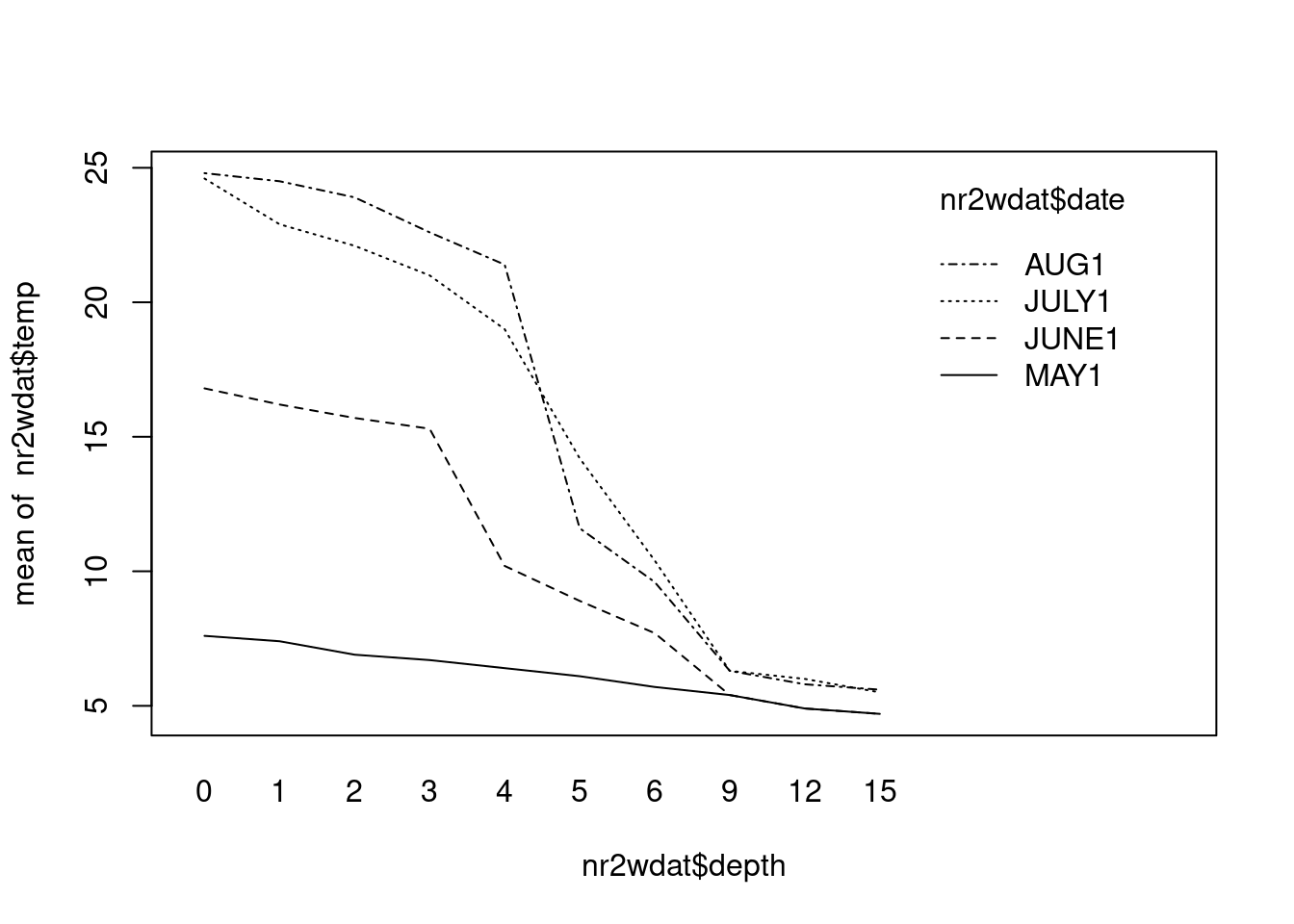

Figure 12.5: Effet du mois et de la profondeur sur la température.

La température diminue significativement en fonction de la profondeur.

Pour tester l’effet du mois (facteur aléatoire), on doit présumer qu’il n’y a pas d’interaction entre la profondeur et le mois (donc que l’effet de la profondeur sur la température est le même à chaque mois).

C’est peu probable: si vous faites un graphique de la température en fonction de la profondeur pour chaque mois, vous observerez que le profil de température change au fur et à mesure du développement de la thermocline. Bref, comme le profil change au cours de l’été, ce modèle ne fait pas de très bonnes prédictions.

Jetez un coup d’oeil aux graphiques des résidus :

par(mfrow = c(2, 2))
plot(anova.model4)

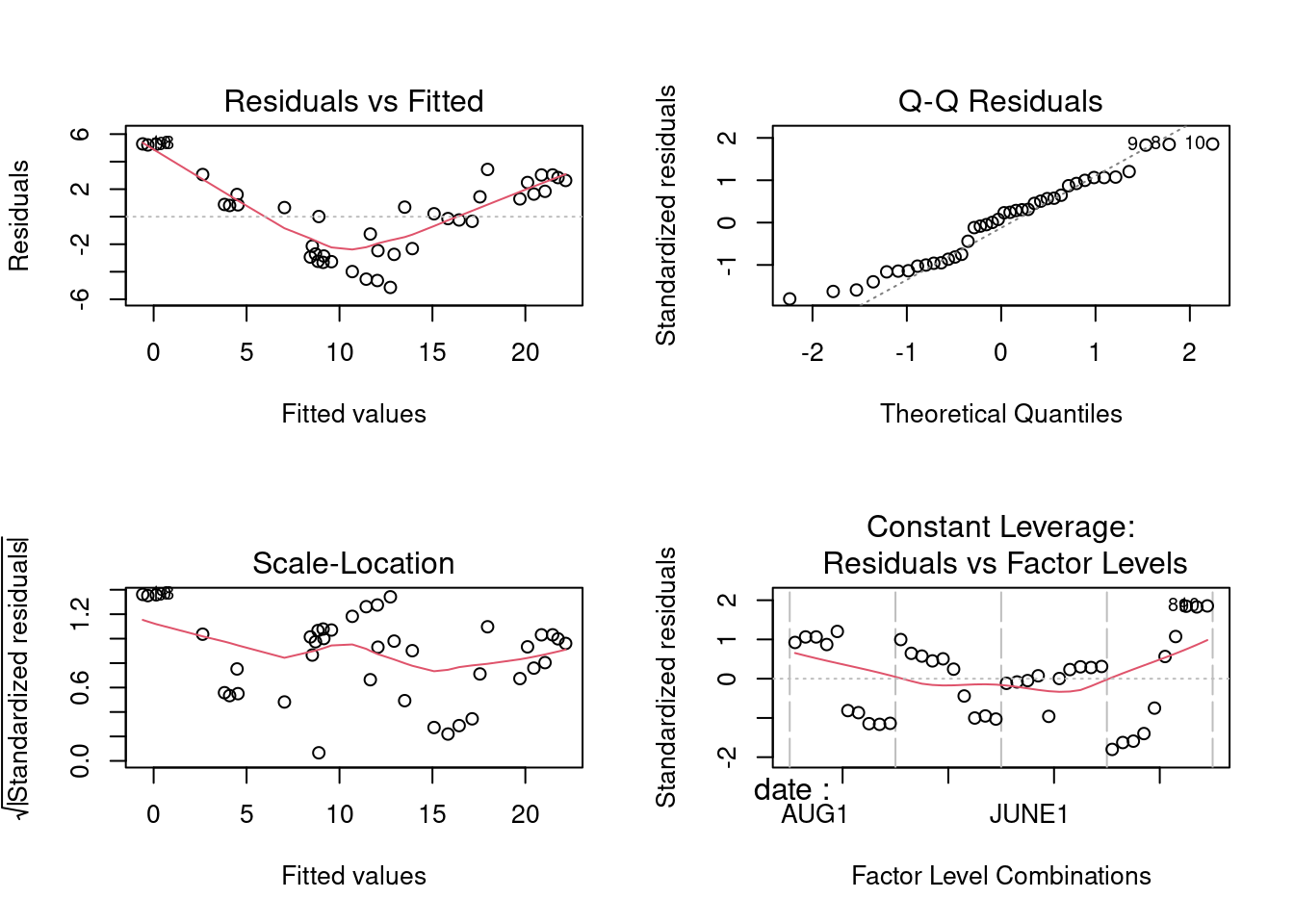
Figure 12.6: Conditions d’applications du modèle `anova.model4`.

shapiro.test(residuals(anova.model4))


    Shapiro-Wilk normality test

data:  residuals(anova.model4)
W = 0.95968, p-value = 0.1634

Le test de normalité sur les résidus donne p = 0.16, donc l’hypothèse de normalité ne semble pas être sérieusement en doute.

Pour l’égalité des variances, on peut seulement comparer entre les mois en utilisant les profondeurs comme réplicats (ou l’inverse). En utilisant les profondeurs comme réplicats, on obtient:

leveneTest(temp ~ date, data = nr2wdat)

Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.

Levene's Test for Homogeneity of Variance (center = median)
      Df F value    Pr(>F)    
group  3  17.979 2.679e-07 ***
      36                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Il y a donc un problème d’hétéroscédasticité, comme on peut très bien voir dans le graphique des résidus vs les valeurs estimées. Cette analyse n’est donc pas très satisfaisante: il y a des violations des conditions d’application et il semble y avoir une interaction entre depth et date qui pourrait invalider l’analyse.

12.4 Plans hiérarchiques

Un design expérimental fréquent implique la division de chaque groupe du facteur majeur en sous-groupes aléatoires.

Par exemple, une généticienne intéressée par l’effet du génotype sur la résistance à la dessiccation chez la drosophile effectue une expérience.

Pour chaque génotype (facteur principal) elle prépare trois chambres de croissance (sous-groupes) avec une température et humidité contrôlées. Dans chaque chambre de croissance, elle place cinq larves, puis mesure le nombre d’heures pendant lesquelles chaque larve survit.

Les données ont donc un structure hiérarchique. Il y a des observations répétées dans chaque chambre au sein de chaque génotype.

Le fichier nestdat.csv contient les résultats d’une expérience semblable. Il contient trois variables : genotype, chamber et survival.

Effectuez une ANOVA hiérarchique avec survival comme variable dépendante et genotype et chamber/genotype comme variables indépendantes.

nestdat <- read.csv("data/nestdat.csv")
nestdat$chamber <- as.factor(nestdat$chamber)
nestdat$genotype <- as.factor(nestdat$genotype)
anova.nested <- lm(survival ~ genotype / chamber, data = nestdat)

Que concluez-vous de cette analyse ? Que devrait être la prochaine étape ?

Indice: si l’effet de genotype / chamber n’est pas significatif, vous pouvez augmenter la puissance des comparaisons entre génotypes en regroupant les chambres de chaque génotype, bien que (y compris Dr. Rundle) n’est pas d’accord avec cette mise en commun. Faites-le ! N’oubliez pas de vérifier les conditions d’applications de l’ANOVA!

Solution

anova(anova.nested)

Analysis of Variance Table

Response: survival
                 Df  Sum Sq Mean Sq  F value Pr(>F)    
genotype          2 2952.22 1476.11 292.6081 <2e-16 ***
genotype:chamber  6   40.65    6.78   1.3432 0.2639    
Residuals        36  181.61    5.04                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1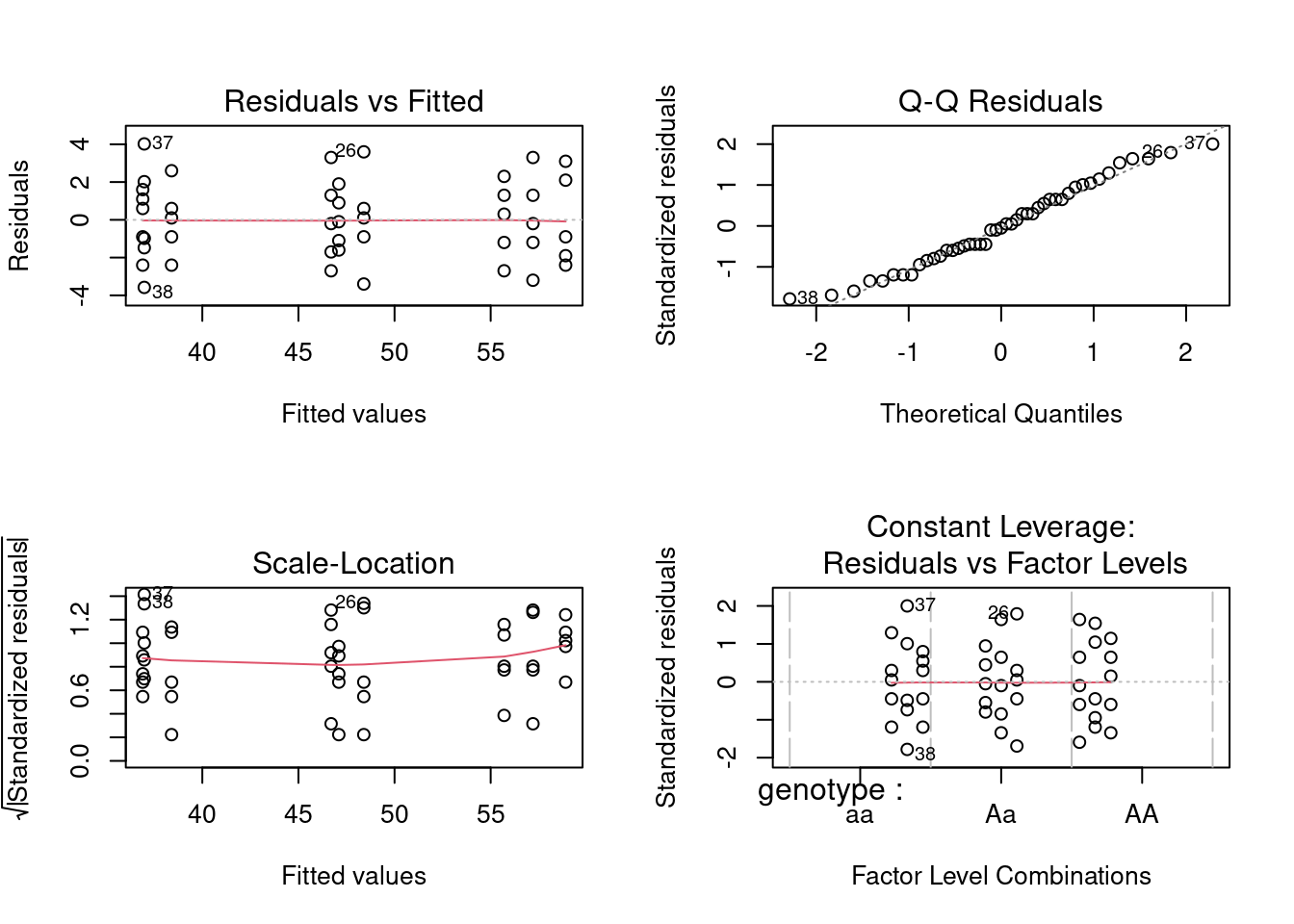

par(mfrow = c(2, 2))
plot(anova.nested)

Figure 12.7: Conditions d’applications du modèle `anova.nested`

On conclue de cette analyse que la variation entre les chambres de croissance n’est pas significative, mais qu’on doit rejeter l’hypothèse nulle que tous les génotypes ont la même résistance à la dessiccation.

Comme l’effet hiérarchique genotype / chamber n’est pas significatif, on peut regrouper les observations pour augmenter le nombre de degrés de liberté :

anova.simple <- lm(survival ~ genotype, data = nestdat)
anova(anova.simple)

Analysis of Variance Table

Response: survival
          Df  Sum Sq Mean Sq F value    Pr(>F)    
genotype   2 2952.22 1476.11  278.93 < 2.2e-16 ***
Residuals 42  222.26    5.29                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Donc on conclue qu’il y a une variation significative de résistance à la dessiccation entre les trois génotypes.

Le graphique de survival en fonction du génotype suggère que la résistance à la dessiccation varie entre chaque génotype. On peut combiner cela avec un test de Tukey.

par(mfrow = c(1, 1))
# Calculer et représenter les moyennes et l'IC de Tukey
means <- glht(anova.simple, linfct = mcp(
  genotype =
    "Tukey"
))
cimeans <- cld(means)
# Utiliser des marges suffisantes
old.par <- par(mai = c(1, 1, 1.25, 1))
# Graphe
plot(cimeans, las = 1) # Argument `las` pour placer les noms d'axes comme Dieu l'a prévu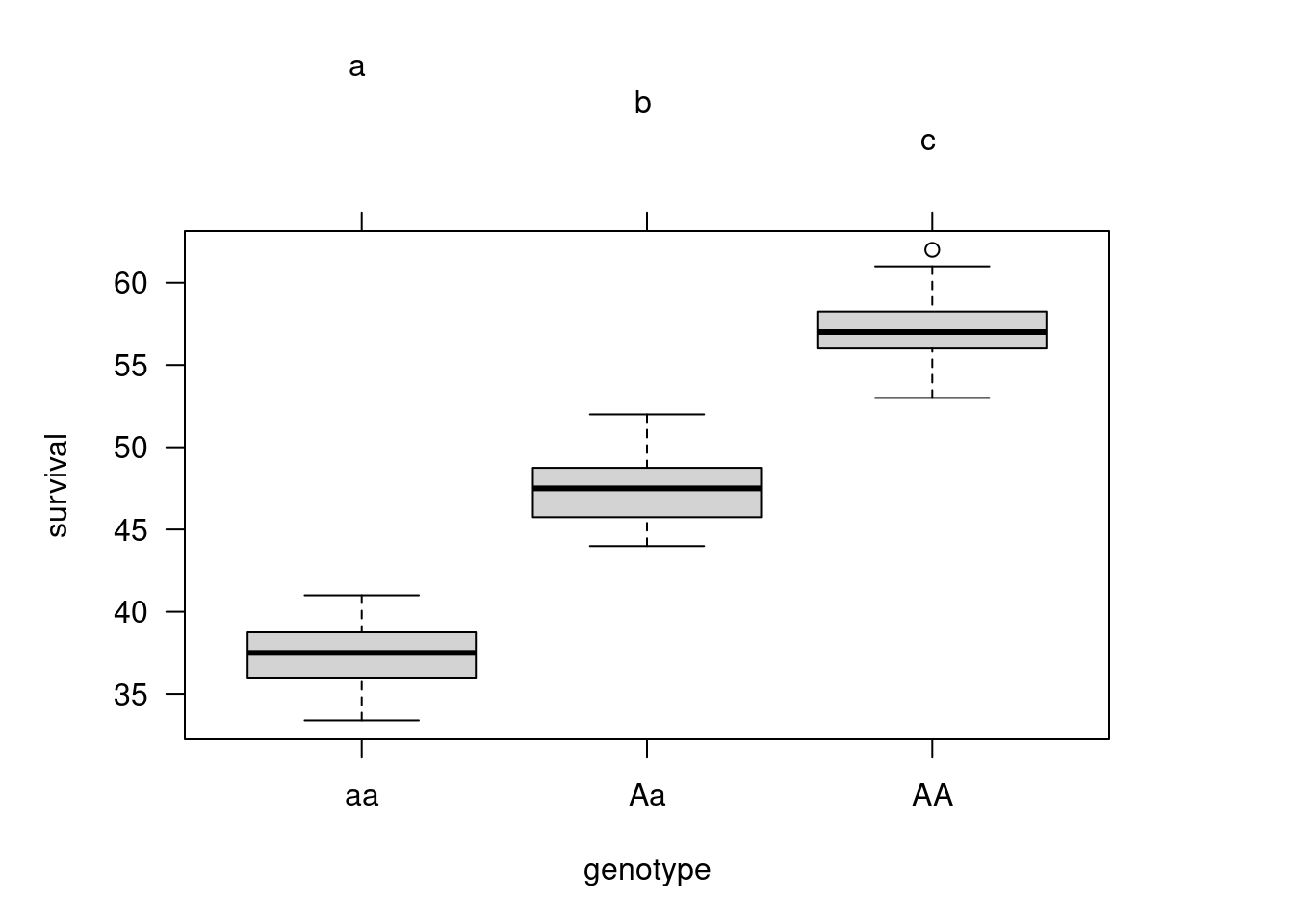

Figure 12.8: Effet du genotype sur la résistance à la dessication avec un test de Tukey.

On conclue donc que la résistance à la dessiccation (R), telle que mesurée par la survie dans des conditions chaudes et sèches, varie significativement entre les trois génotypes avec R(AA) > R(Aa) > R(aa).

Cependant, avant d’accepter cette conclusion, il faut éprouver les conditions d’application du test.

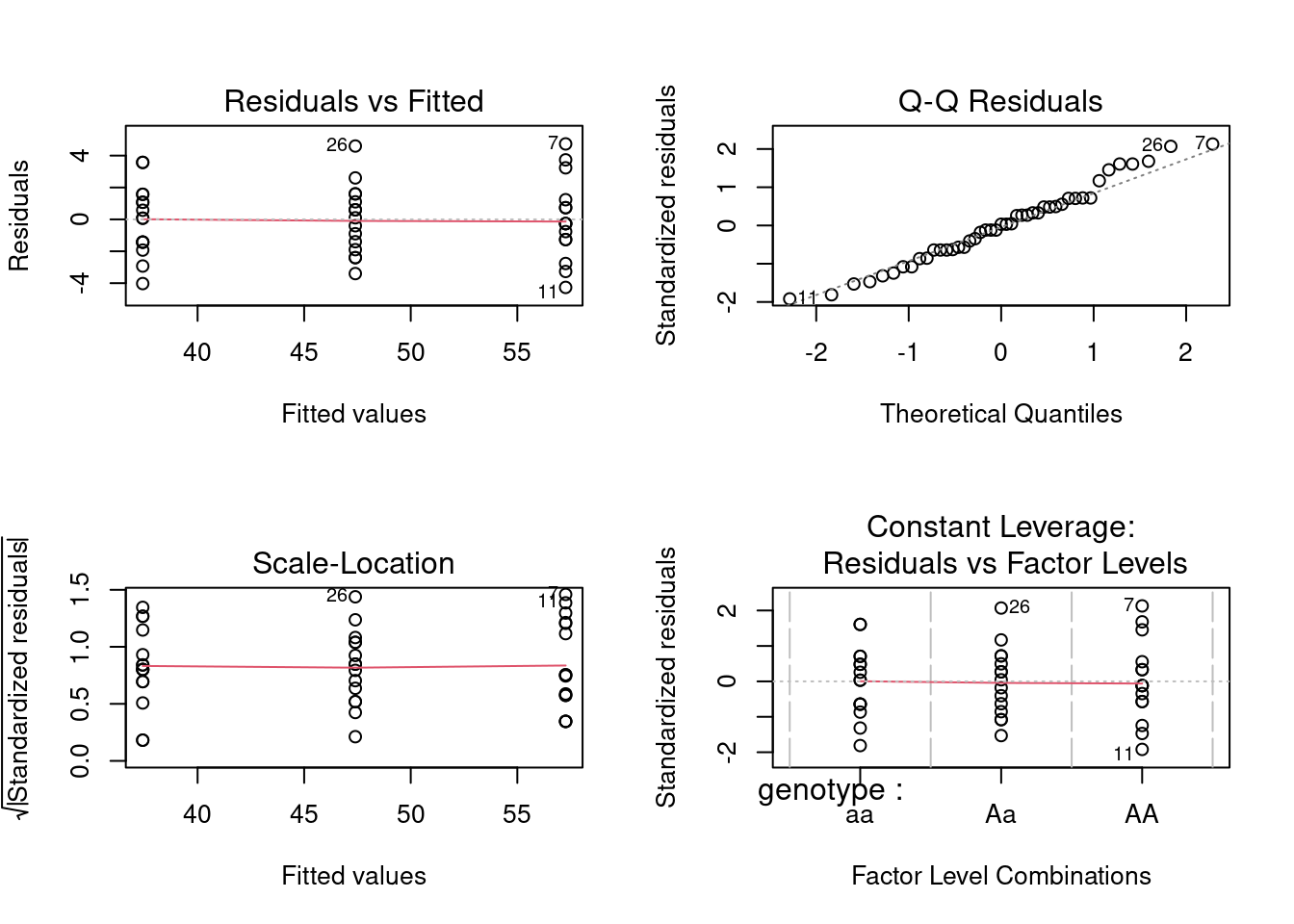
Voici les diagnostics des résidus pour l’ANOVA à un critère de classification (non hiérarchique):

Solution

par(mfrow = c(2, 2))
plot(anova.simple)

Figure 12.9: Conditions d’applications du modèle anova.simple

Donc, toutes les conditions d’application semblent être remplies, et on peut donc accepter les conclusions. Notez que si l’on compare le carré moyen des résidus de l’ANOVA hiérarchique et de l’ANOVA à un critère de classification (5.045 vs 5.292), ils sont presque identiques. Cela n’est pas surprenant compte tenu de la faible variabilité associée aux chambres de croissance pour chaque génotype.

12.5 ANOVA non paramétrique avec 2 facteurs de classification

L’ANOVA non paramétrique à 2 critères de classification est une extension de celle à 1 critère de classification vue précédemment. Elle débute par une ANOVA faite sur les données transformées en rangs. Elle peut se faire sur des données avec ou sans réplicats.

À partir du fichier stu2wdat.csv, effectuez une ANOVA non paramétrique à 2 facteurs de classification pour examiner l’effet de sex et location sur rank(rdwght).

aov.rank <- aov(
  rank(rdwght) ~ sex * location,
  contrasts = list(
    sex = contr.sum, location = contr.sum
  ),
  data = Stu2wdat
)

L’extension de Schreirer-Ray-Hare au test de Kruskall-Wallis se fait en calculant une statistique H donnée par la somme des carrés de l’effet divisé par la somme des carrés totale (qui peut être calculé comme la variance des rangs). On calcule ensuite cette statistique H pour chaque terme, pour ensuite les comparer à une distribution théorique de $\chi^2$ (chi-carré) en utilisant la commande pchisq(H, df, lower.tail = FALSE), où H et df sont les statistiques H calculées et les degrés de libertés, respectivement.

Testez l’effet de sex et location sur rdwght. Que concluez-vous ? Comment ce résultat se compare-t-il à celui obtenu en faisant l’ANOVA paramétrique faite précédemment ?

Anova(aov.rank, type = 3)

Anova Table (Type III tests)

Response: rank(rdwght)
              Sum Sq  Df  F value    Pr(>F)    
(Intercept)  1499862   1 577.8673 < 2.2e-16 ***
sex            58394   1  22.4979 4.237e-06 ***
location        1128   1   0.4347    0.5105    
sex:location    1230   1   0.4738    0.4921    
Residuals     472383 182                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pour calculer l’extension Schreirer-Ray-Hare au test de Kruskall-Wallis, on doit d’abord calculer le carré moyen total (i.e., la variance des données transformées en rang. Ici, on a 186 observations, donc des rangs; 1, 2, 3, … 186).

La variance de cette série de 186 valeurs peut être calculée simplement par var(1:186).

Donc on peut calculer la statistique H pour chaque terme:

Hsex <- 58394 / var(1:186)
Hlocation <- 1128 / var(1:186)
Hsexloc <- 1230 / var(1:186)

Et convertir ces statistiques en valeur de p :

# sex
Hsex

[1] 20.14628

pchisq(Hsex, 1, lower.tail = FALSE)

[1] 7.173954e-06

# location
Hlocation

[1] 0.3891668

pchisq(Hlocation, 1, lower.tail = FALSE)

[1] 0.5327377

# sex:location
Hsexloc

[1] 0.4243574

pchisq(Hsexloc, 1, lower.tail = FALSE)

[1] 0.5147707

Ces résultats sont semblables aux résultats de l’ANOVA non-paramétrique à 2 critères de classification. Malgré la puissance réduite, il y a encore un effet significatif du sexe, mais ni interaction ni effet du site.

Il y a cependant un différence importante. Rappelez-vous que dans l’ANOVA paramétrique d’origine, il y avait un effet significatif du sexe en considérant le problème comme une ANOVA Modèle I (fixe). Mais, si nous le considérons comme un modèle III (mixte), l’effet significatif du sexe pourrait en principe disparaître, car les degrées de liberté (ddl) associés au carré moyen (CM) de l’interaction sont plus faibles que le nombre de ddl du CM de l’erreur du modèle à effet fixes. Dans ce cas ci, cependant, le CM de l’interaction est environ la moitié du CM de l’erreur. Par conséquent, l’effet significatif de sex pourrait devenir encore plus significatif si le problème est analysé (comme il se doit) comme une ANOVA mixte. Encore une fois on peut voir l’importance de spécifier le modèle adéquat en ANOVA.

12.6 Comparaisons multiples

Les épreuves d’hypothèses subséquentes en ANOVA à plus d’un critère de classification dépendent des résultats initiaux de l’ANOVA. Si vous êtes intéressés à comparer des effets moyens d’un facteur pour tous les niveaux d’un autre facteur (par exemple l’effet du sexe sur la taille des esturgeons peu importe d’où ils viennent), alors vous pouvez procéder exactement tel que décrit dans la section sur les comparaisons multiples suivant l’ANOVA à un critère de classification. Pour comparer les moyennes des cellules entre elles, il faut spécifier l’interaction comme variable qui représente le groupe.

Le fichier wmcdat2.csv contient des mesures de consommation d’oxygène, o2cons, de deux espèces, species, d’un mollusque (une patelle) à trois concentrations différentes d’eau de mer (donc de salinité), conc. Ces données sont présentées à la p. 332 de Sokal et Rohlf 1995.

Effectuez une ANOVA factorielle à 2 critères de classification sur ces données en utilisant o2cons comme variable dépendante et species et conc comme les facteurs (il va probablement falloir changer le type de données de variable conc à facteur). Que concluez-vous ?

Solution

wmcdat2 <- read.csv("data/wmcdat2.csv")
wmcdat2$species <- as.factor(wmcdat2$species)
wmcdat2$conc <- as.factor(wmcdat2$conc)
anova.model5 <- lm(o2cons ~ species * conc, data = wmcdat2)
Anova(anova.model5, type = 3)

Anova Table (Type III tests)

Response: o2cons
              Sum Sq Df  F value    Pr(>F)    
(Intercept)  1185.60  1 124.0165 4.101e-14 ***
species         0.09  1   0.0097   0.92189    
conc           74.90  2   3.9172   0.02755 *  
species:conc   23.93  2   1.2514   0.29656    
Residuals     401.52 42                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Comme l’effectif dans chaque cellule est relativement petit, il faudrait idéalement refaire cette analyse avec une ANOVA non-paramétrique. Pour le moment, contentons nous de la version paramétrique.

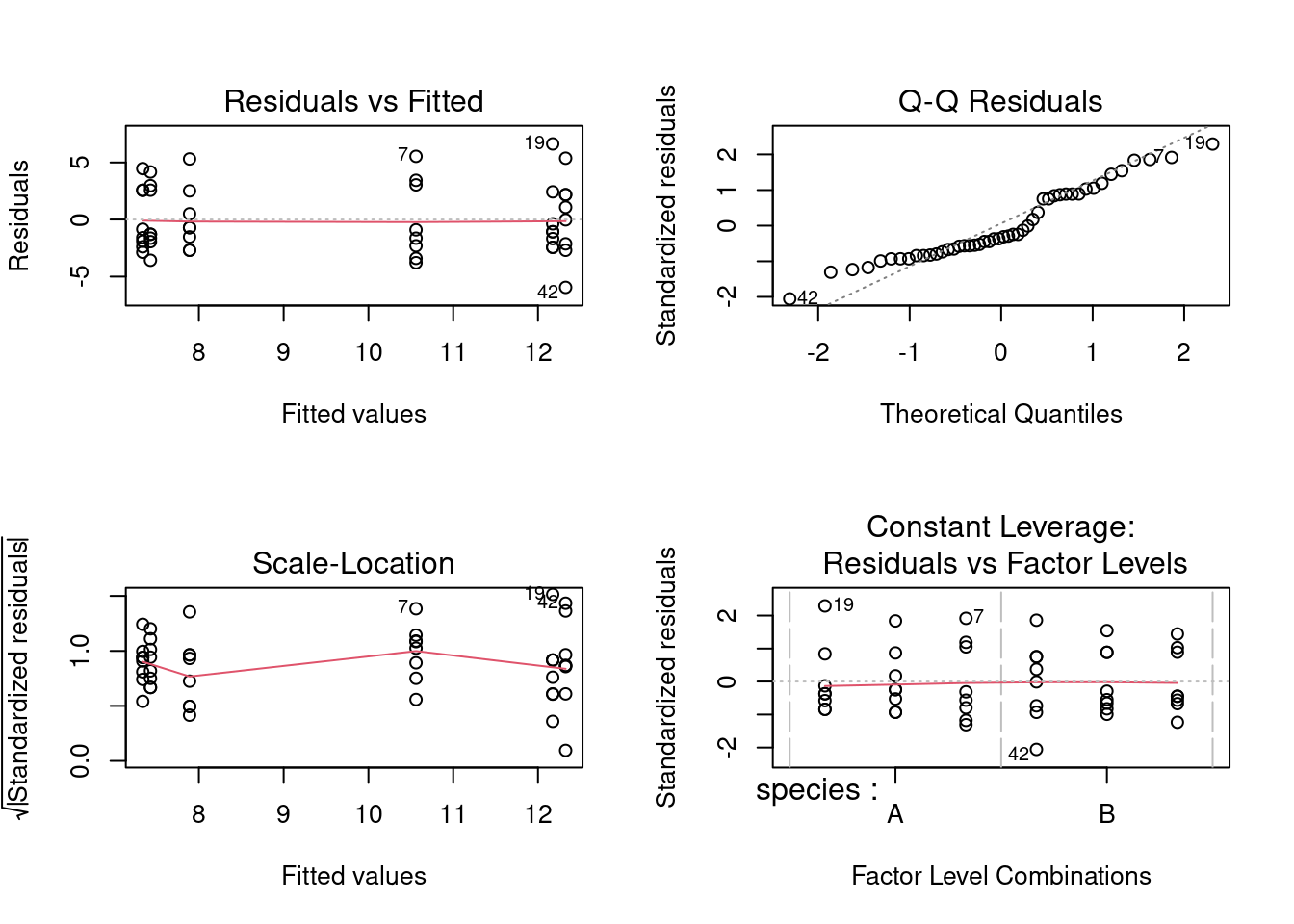
Examinons les graphiques diagnostiques:

Solution

par(mfrow = c(2, 2))
plot(anova.model5)

Les variances semblent égales.

Le test de normalité donne:

Solution

shapiro.test(residuals(anova.model5))


    Shapiro-Wilk normality test

data:  residuals(anova.model5)
W = 0.93692, p-value = 0.01238

Il y a un écart à la normalité, mais à part ça tout semble aller. Comme l’ANOVA est relativement robuste à la non-normalité, on va regarder de l’autre coté (Si vous voulez être plus confiants, vous pouvez tourner une ANOVA non paramétrique. Vous arriverez aux mêmes conclusions.)

On conclue donc qu’il n’y a pas de différence entre les espèces et que l’effet de la concentration ne dépends pas de l’espèce (il n’y a pas d’interaction). Par conséquent, les seules comparaisons justifiables sont entre les concentrations :

# Ajuster un modèle simplifié
anova.model6 <- aov(o2cons ~ conc, data = wmcdat2)
# Faire de comparaisons multiple de Tuley
TukeyHSD(anova.model6)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = o2cons ~ conc, data = wmcdat2)

$conc
           diff       lwr        upr     p adj
75-50  -4.63625 -7.321998 -1.9505018 0.0003793
100-50 -3.25500 -5.940748 -0.5692518 0.0141313
100-75  1.38125 -1.304498  4.0669982 0.4325855

par(mfrow = c(1, 1))
# Graphique de toutes les comparaions pour `conc`
tuk <- glht(anova.model6, linfct = mcp(conc = "Tukey"))
# Extraire l'information
tuk.cld <- cld(tuk)
# Utiliser des marges suffisantes
old.par <- par(mai = c(1, 1, 1.25, 1))
# Graphe
plot(tuk.cld)
par(old.par)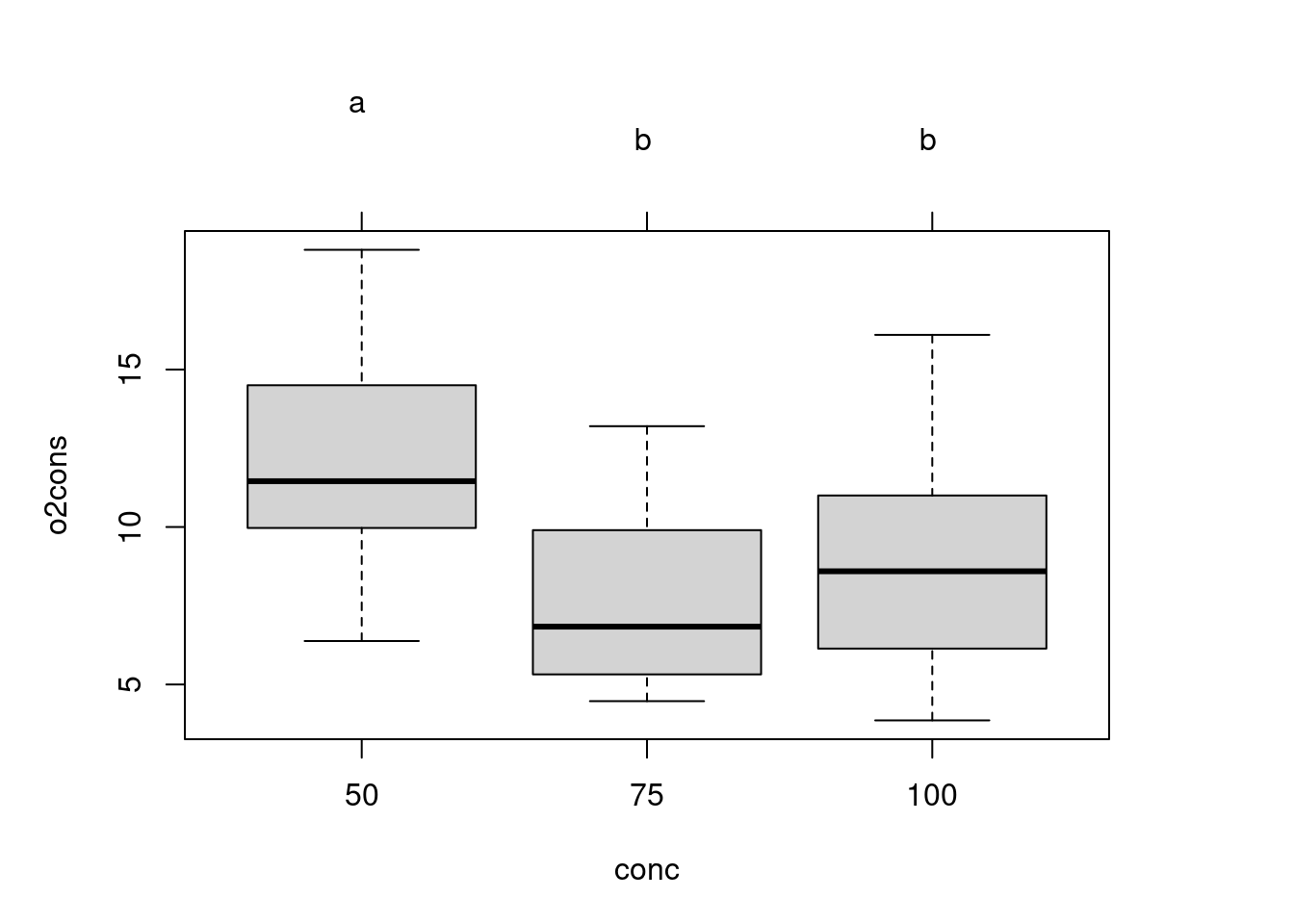

Figure 12.11: Comparaison de Tukey des moyennes de consommation d’oxygèn en fonction del la concentration

Il y a donc une différence de consommation d’oxygène significative lorsque la salinité est réduite de 50%, mais pas à 25% de réduction.

Répétez les deux analyses précédentes sur les données du fichier wmc2dat2.csv. Comment les résultats se comparent-ils à ceux obt$nus précédemment ?

Solution

wmc2dat2 <- read.csv("data/wmc2dat2.csv")
wmc2dat2$species <- as.factor(wmc2dat2$species)
wmc2dat2$conc <- as.factor(wmc2dat2$conc)
anova.model7 <- lm(o2cons ~ species * conc, data = wmc2dat2)

En utilisant wmc2dat2.csv, on obtient:

Anova Table (Type III tests)

Response: o2cons
             Sum Sq Df F value    Pr(>F)    
(Intercept)  343.09  1 36.2132 3.745e-07 ***
species      133.52  1 14.0929 0.0005286 ***
conc          66.76  2  3.5232 0.0385011 *  
species:conc 168.15  2  8.8742 0.0006101 ***
Residuals    397.91 42                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dans ce cas ci, il y a une interaction significative, et il n’est par conséquent pas approprié de comparer les moyennes regroupées par espèce ou concentration. Ceci est clairement visualisé par un graphique d’interaction:

with(wmc2dat2, interaction.plot(conc, species, o2cons))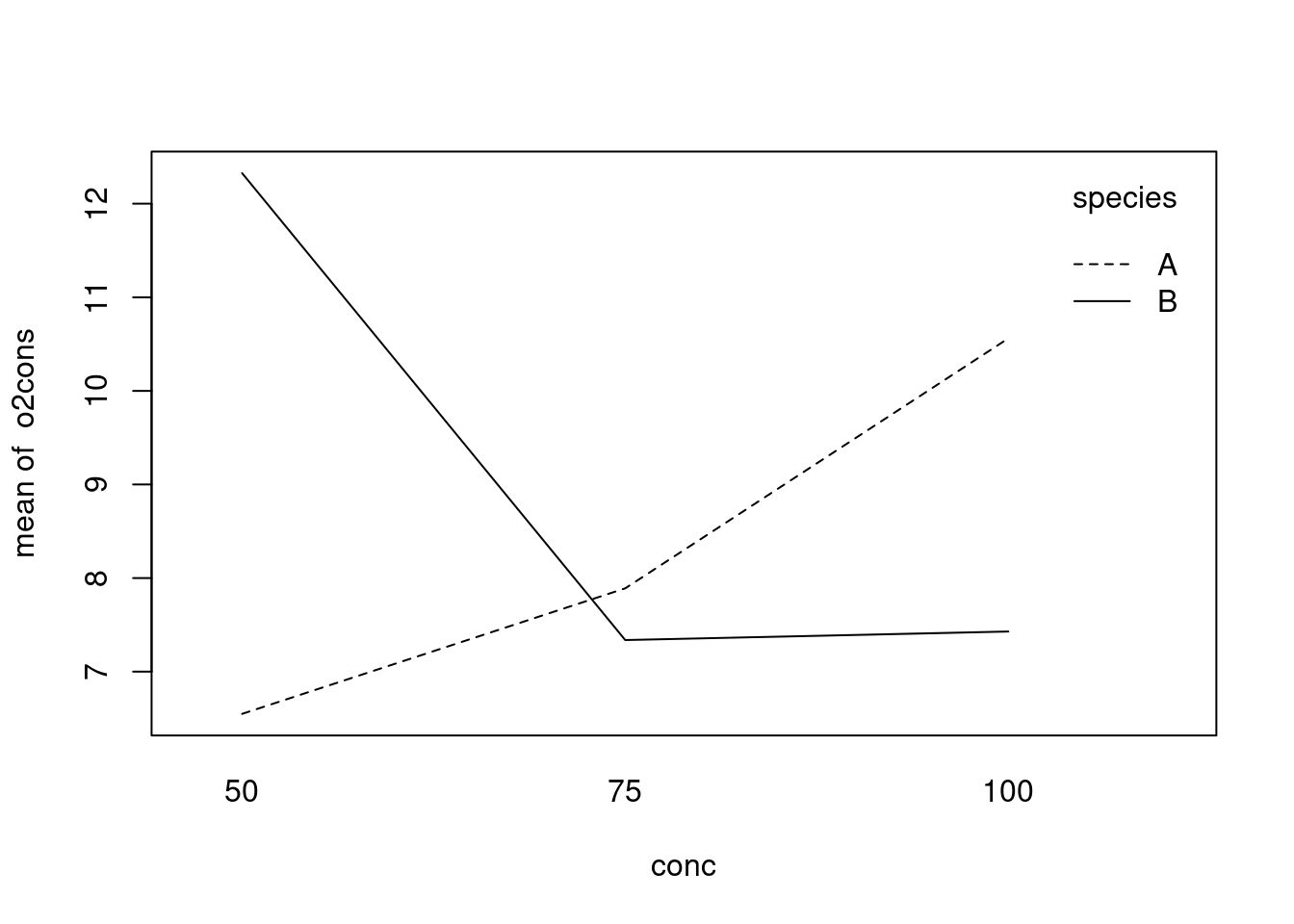

Toujours en utilisant les données de wmc2dat2.csv, comparez les 6 moyennes avec l’ajustement Bonferonni. Pour ce faire, il sera utile de créer une nouvelle variable qui combine species et conc:

wmc2dat2$species.conc <- as.factor(paste0(wmc2dat2$species, wmc2dat2$conc))

ensuite on peut faire les comparaisons de Bonferroni:

with(wmc2dat2, pairwise.t.test(o2cons, species.conc, p.adj = "bonf"))


    Pairwise comparisons using t tests with pooled SD 

data:  o2cons and species.conc 

     A100   A50    A75    B100   B50   
A50  0.1887 -      -      -      -     
A75  1.0000 1.0000 -      -      -     
B100 0.7223 1.0000 1.0000 -      -     
B50  1.0000 0.0079 0.0929 0.0412 -     
B75  0.6340 1.0000 1.0000 1.0000 0.0350

P value adjustment method: bonferroni

Ces comparaisons sont un peu plus difficiles à interpréter, mais l’analyse porte essentiellement sur les différences entre les concentrations d’eau de mer au sein de l’espèce A et sur les différences entre les concentrations au sein de l’espèce B. Nous voyons ici que la consommation d’oxygène à 50% d’eau de mer pour l’espèce B et significativement différente par rapport à 75% et 100% d’eau de mer. Là où il n’y a pas de différences significatives pour l’espèce A selon les concentrations.

Je trouve ces tableaux de résultats peu satisfaisants parce qu’ils indiquent seulement les valeur de p sans indices de la taille de l’effet. On peut obtenir à la fois le résultat des tests de comparaison multiple et un indice de la taille de l’effet à l’aide du code suivant :

# Ajuster un ANOVA a 2 facteurs pour toutes les combinaisons espèce.concentration
anova.modelx <- aov(o2cons ~ species.conc, data = wmc2dat2)
tuk2 <- glht(anova.modelx, linfct = mcp(species.conc = "Tukey"))
# Extraire l'information
tuk2.cld <- cld(tuk2)
# Utiliser des marges suffisantes
old.par <- par(mai = c(1, 1, 1.25, 1))
# Graphes
plot(tuk2.cld)
par(old.par)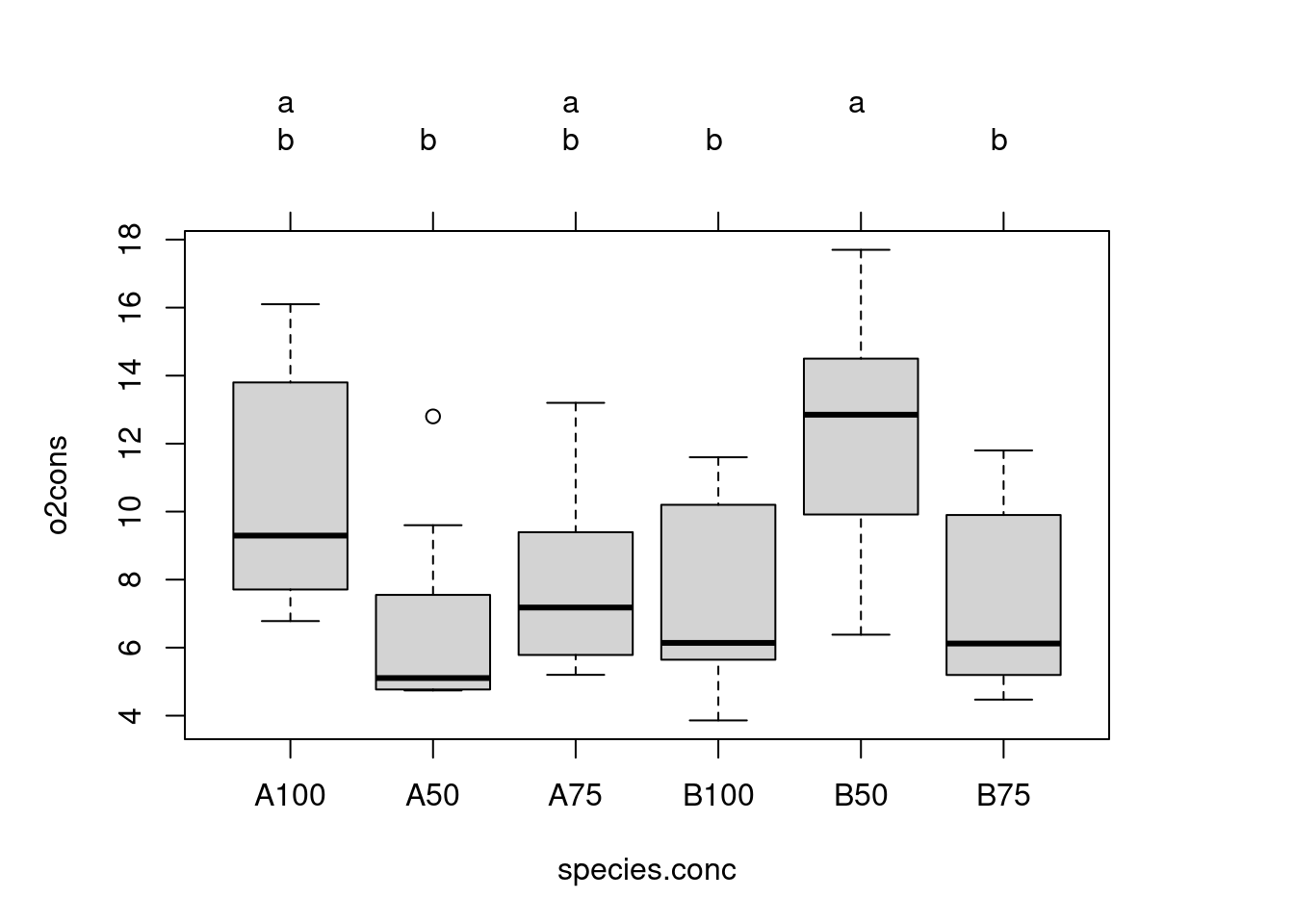

Dans cette analyse on a utilisé le CM = 9.474 du modèle d’ANOVA pour comparer les moyennes. En faisant ça, on présume qu’il s’agit d’une situation d’ANOVA à effet fixes, ce qui n’est peut-être pas le cas (conc est certainement fixe, mais species peut être fixe ou aléatoire).

12.7 Test de permutation pour l’ANOVA à 2 facteurs de classification

Quand les données ne répondent pas aux conditions d’applications d’une ANOVA paramétrique à 2 ou plusieurs facteurs de classification, il est possible, comme alternative à l’ANOVA non-paramétrique, de faire des tests de permutation pour calculer les valeurs p.

###########################################################
# Test de permutation pour une ANOVA à 2 facteurs
# Ter Braak crée des résidus à partir des moyennes des cellules,
# puis effectue des permutations entre toutes les cellules
# Cela peut être fait en prenant les résidus du modèle complet.
# modifié depuis le code écrit par David C. Howell
# http://www.uvm.edu/~dhowell/StatPages/More_Stuff/Permutation%20Anova/PermTestsAnova.html
nreps <- 500
dependent <- Stu2wdat$rdwght
factor1 <- as.factor(Stu2wdat$sex)
factor2 <- as.factor(Stu2wdat$location)
my.dataframe <- data.frame(dependent, factor1, factor2)
my.dataframe.noNA <- my.dataframe[complete.cases(my.dataframe), ]
mod <- lm(dependent ~ factor1 + factor2 + factor1:factor2,
  data = my.dataframe.noNA
)
res <- mod$residuals
TBint <- numeric(nreps)
TB1 <- numeric(nreps)
TB2 <- numeric(nreps)
ANOVA <- summary(aov(mod))
cat(
  " L'ANOVA standard pour ces données suit ",
  "\n"
)
F1 <- ANOVA[[1]]$"F value"[1]
F2 <- ANOVA[[1]]$"F value"[2]
Finteract <- ANOVA[[1]]$"F value"[3]
print(ANOVA)
cat("\n")
cat("\n")
TBint[1] <- Finteract
for (i in 2:nreps) {
  newdat <- sample(res, length(res), replace = FALSE)
  modb <- summary(aov(newdat ~ factor1 + factor2 +
    factor1:factor2,
  data = my.dataframe.noNA
  ))
  TBint[i] <- modb[[1]]$"F value"[3]
  TB1[i] <- modb[[1]]$"F value"[1]
  TB2[i] <- modb[[1]]$"F value"[2]
}
probInt <- length(TBint[TBint >= Finteract]) / nreps
prob1 <- length(TB1[TB1 >= F1]) / nreps
prob2 <- length(TB2[TB1 >= F2]) / nreps
cat("\n")
cat("\n")
print("Rééchantillonnage comme dans ter Braak avec rééchantillone non restraint des cellules résiduelles. ")
cat(
  "La probabilité pour l'effet d'Interaction est ",
  probInt, "\n"
)
cat(
  "La probabilité pour l'effet du Facteur 1 est ",
  prob1, "\n"
)
cat(
  "La probabilité pour l'effet du Facteur 2 est ",
  prob2, "\n"
)

Avec le paquet lmPerm 📦, vous pouvez effectuer le test de permutation beaucoup plus rapidement et facilement :

#######################################################################
## Test de permutation version `lmPerm`
library(lmPerm)
# Par soucis de généralisation, assignez votre jeu de donnée à l'objet "mesdonnees"
# et la formule du modèle à "maformule"
mesdonnees <- Stu2wdat
maformule <- as.formula("rdwght ~ sex+location+sex:location")
# Ajustez le modèle voulu aux données voulues
monmodele <- lm(maformule, data = mesdonnees)
# Calculez la valeur p permutée
anova(lmp(maformule, data = mesdonnees, perm = "Prob", center = FALSE, Ca = 0.001))

12.8 Bootstrap pour l’ANOVA à 2 facteurs de classification

Dans la plupart des cas, les tests de permutation seront plus appropriés que le bootstrap pour les ANOVA. J’ai quand même un bout de code qui pourra servir si vous en avez besoin:

############################################################
###########
# Bootstrap pour une ANOVA à 2 facteurs
# Vous aurez peut être envie de modifier "bootfunction.mod1" pour renvoyer d'autres valeurs
# Ici, ça renvoie les coefficients standard du modèle ajusté
# Requiert le paquet `boot`
#
nreps <- 5000
dependent <- Stu2wdat$rdwght
factor1 <- as.factor(Stu2wdat$sex)
factor2 <- as.factor(Stu2wdat$location)
my.dataframe <- data.frame(dependent, factor1, factor2)
my.dataframe.noNA <- my.dataframe[complete.cases(my.dataframe), ]
library(boot)
# Ajustez le modèle aux données observées
mod1 <- aov(dependent ~ factor1 + factor2 + factor1:factor2,
  data = my.dataframe.noNA
)


# Bootstrap 1000 fois en utilisant la méthode de bootstraping résiduel pour
# garder le même nombre inégal d'observations pour chaque niveaux de la variable indépendante.
fit <- fitted(mod1)
e <- residuals(mod1)
X <- model.matrix(mod1)
bootfunction.mod1 <- function(data, indices) {
  y <- fit + e[indices]
  bootmod <- lm(y ~ X)
  coefficients(bootmod)
}
bootresults <- boot(my.dataframe.noNA, bootfunction.mod1,
  R = 1000
)
bootresults
## Calcule l'IC 90% et trace les estimés du bootstrap séparément pour chaque paramètres du modèle
boot.ci(bootresults, conf = 0.9, index = 1)
plot(bootresults, index = 1)
boot.ci(bootresults, conf = 0.9, index = 3)
plot(bootresults, index = 3)
boot.ci(bootresults, conf = 0.9, index = 4)
plot(bootresults, index = 4)
boot.ci(bootresults, conf = 0.9, index = 5)
plot(bootresults, index = 5)