11  ANOVA à un critère de classification

Objectifs de ce chapitre :

11.1 Paquets et données requises pour le labo

Pour ce laboratoire, vous aurez besoin de :

  • Paquets R :
    • ggplot2 📦
    • multcomp 📦
    • car 📦
  • Jeu de données :
    • “Dam10dat.csv”

11.2 ANOVA à un critère de classification et comparaisons multiples

L’ANOVA à un critère de classification est l’analogue du test de t pour des comparaisons de moyennes de plus de deux échantillons. Les conditions d’application du test sont essentiellement les mêmes, et lorsque appliqué à deux échantillons ce test est mathématiquement équivalent au test de t.

En 1961-1962, le barrage Grand Rapids était construit sur la rivière Saskatchewan en amont de Cumberland House. Certains rapports indiqueraient que durant la construction, plusieurs gros esturgeons restèrent prisonniers dans des sections peu profondes et moururent. Des inventaires de la population d’esturgeons furent faits en 1954, 1958, 1965 et 1966. Au cours de ces inventaires, la longueur à la fourche (frklngth) a été mesurée (pas nécessairement sur chaque poisson cependant). Ces données sont contenues dans le fichier Dam10dat.csv.

11.2.1 Visualiser les données

  • À partir des données (Dam10dat), il faut d’abord changer le type de donnée de la variable year, pour que R la traite comme un facteur (as.factor()) plutôt que comme une variable continue.
Dam10dat <- read.csv("data/Dam10dat.csv")
Dam10dat$year <- as.factor(Dam10dat$year)
str(Dam10dat)
'data.frame':   118 obs. of  21 variables:
 $ year    : Factor w/ 4 levels "1954","1958",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ fklngth : num  45 50 39 46 54.5 49 42.5 49 56 54 ...
 $ totlngth: num  49 NA 43 50.5 NA 51.7 45.5 52 60.2 58.5 ...
 $ drlngth : logi  NA NA NA NA NA NA ...
 $ drwght  : num  16 20.5 10 17.5 19.7 21.3 9.5 23.7 31 27.3 ...
 $ rdwght  : num  24.5 33 15.5 28.5 32.5 35.5 15.3 40.5 51.5 43 ...
 $ sex     : int  1 1 1 2 1 2 1 1 1 1 ...
 $ age     : int  24 33 17 31 37 44 23 34 33 47 ...
 $ lfkl    : num  1.65 1.7 1.59 1.66 1.74 ...
 $ ltotl   : num  1.69 NA 1.63 1.7 NA ...
 $ ldrl    : logi  NA NA NA NA NA NA ...
 $ ldrwght : num  1.2 1.31 1 1.24 1.29 ...
 $ lrdwght : num  1.39 1.52 1.19 1.45 1.51 ...
 $ lage    : num  1.38 1.52 1.23 1.49 1.57 ...
 $ rage    : int  4 6 3 6 7 7 4 6 6 7 ...
 $ ryear   : int  1954 1954 1954 1954 1954 1954 1954 1954 1954 1954 ...
 $ ryear2  : int  1958 1958 1958 1958 1958 1958 1958 1958 1958 1958 ...
 $ ryear3  : int  1966 1966 1966 1966 1966 1966 1966 1966 1966 1966 ...
 $ location: int  1 1 1 1 1 1 1 1 1 1 ...
 $ girth   : logi  NA NA NA NA NA NA ...
 $ lgirth  : logi  NA NA NA NA NA NA ...
  • Ensuite, visualisez les données (de la même manière que dans le chapitre précédent sur les tests de t). Créez un histogramme avec une courbe de densité et un “Box plot” par année. Que vous révèlent ces données ?
mongraph <- ggplot(Dam10dat, aes(x = fklngth)) +
  labs(x = "Longueur à la fourche (cm)",
       y = "Densité") +
  geom_density() +
  geom_rug() +
  geom_histogram(aes(y = after_stat(density)),
    color = "black",
    alpha = 0.3
  ) +
  stat_function(
    fun = dnorm,
    args = list(
      mean = mean(Dam10dat$fklngth),
      sd = sd(Dam10dat$fklngth)
    ),
    color = "red"
  )

# Affichez le graphe, par année
mongraph + facet_wrap(~year, ncol = 2)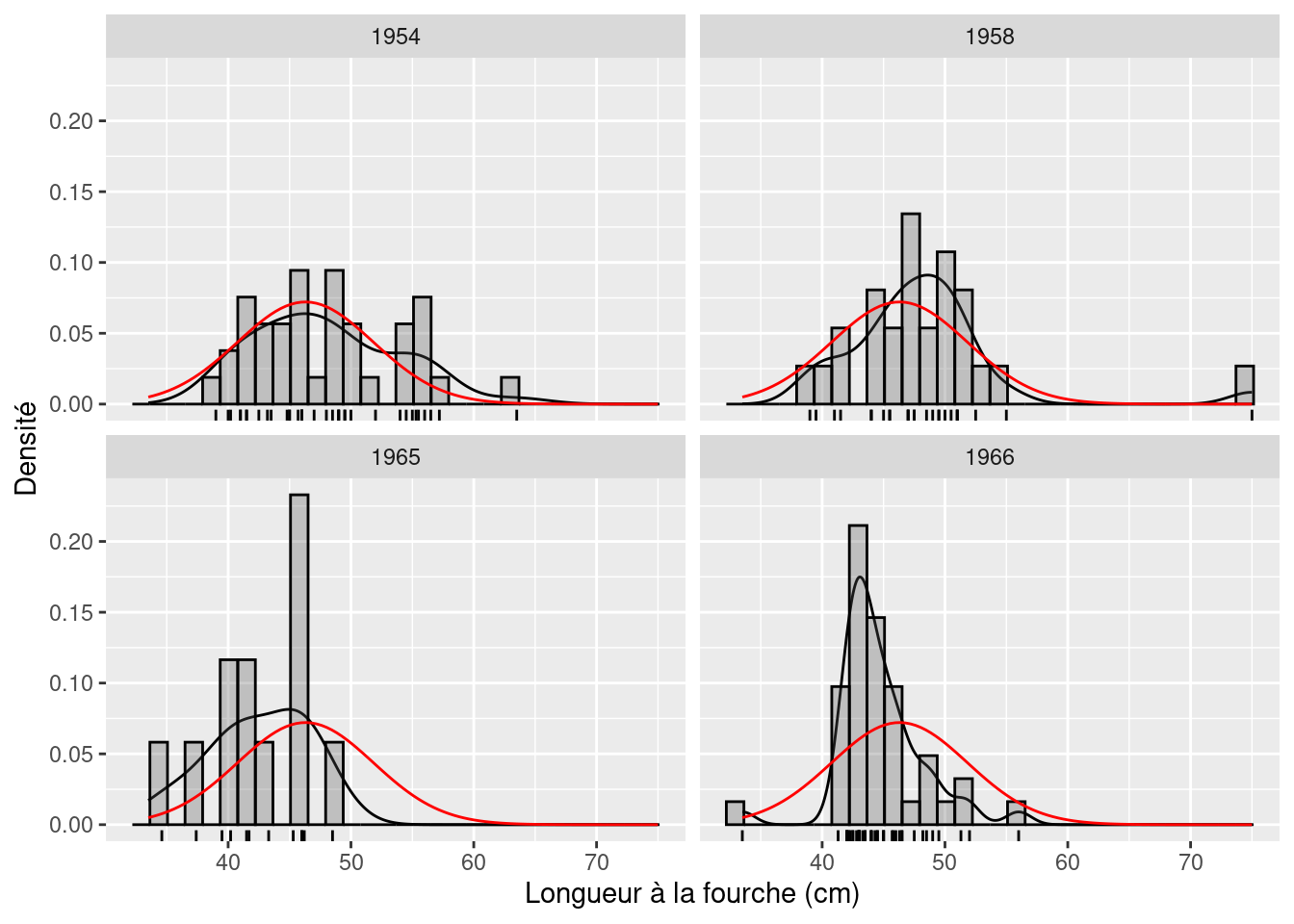
Figure 11.1: Distribution de la longueur des esturgeons par année. 
boxplot(fklngth ~ year, data = Dam10dat,
        xlab = "Années", ylab = "Longueur à la fourche (cm)")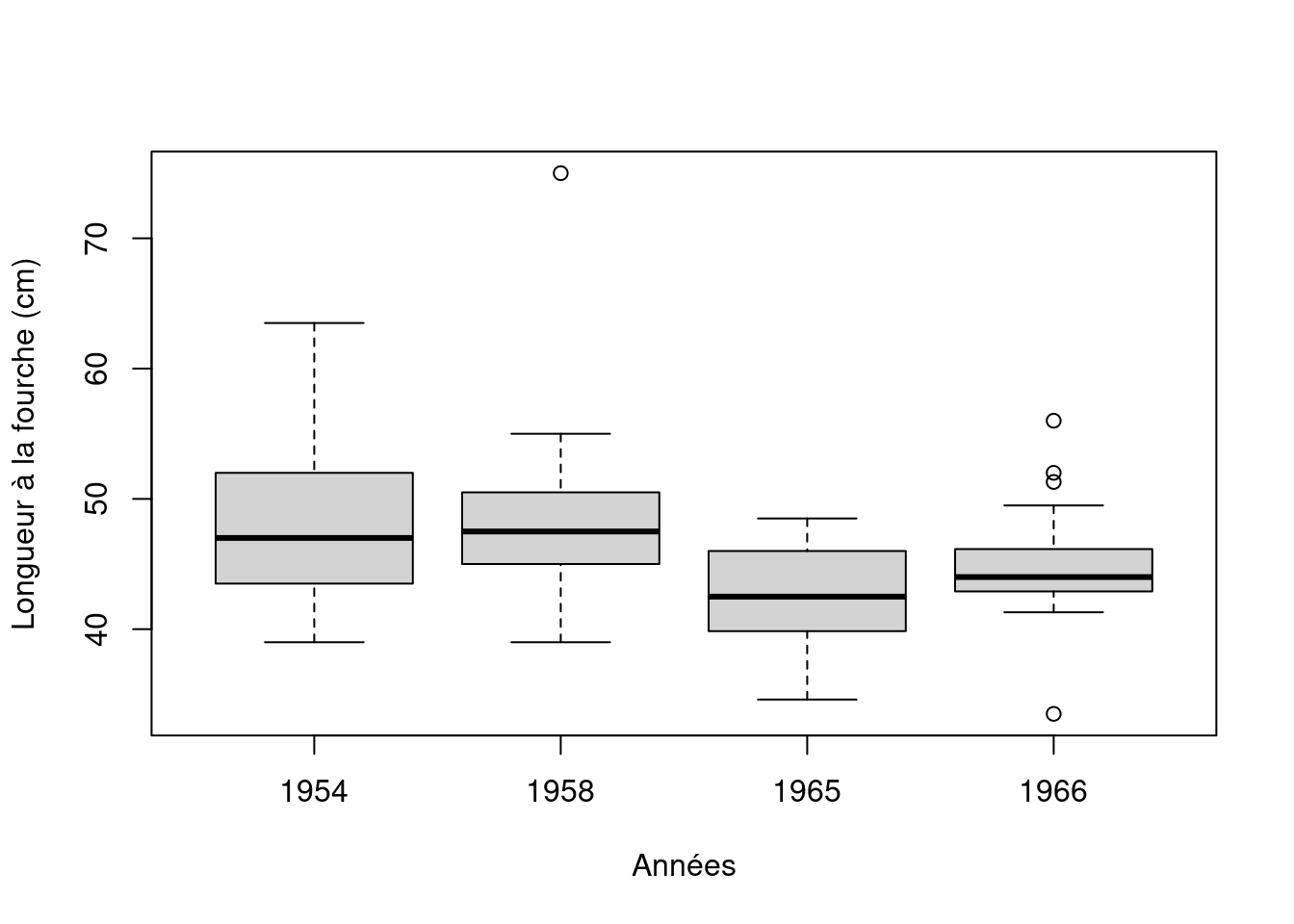
Figure 11.2: Boxplot de la longueur à la fourche pas annéee.

Il semble que la taille des esturgeons ait légèrement diminué après la construction du barrage, mais les données sont très variables et les effets ne sont pas parfaitement clairs. Il y a peut-être des problèmes de normalité avec les échantillons de 1954 et 1966, et il y a probablement des valeurs extrêmes dans les échantillons de 1958 et 1966. Testons les conditions d’application de l’ANOVA. Il faut d’abord faire l’analyse et examiner les résidus.

11.2.2 Vérifier les conditions d’application de l’ANOVA paramétrique

L’ANOVA paramétrique a trois principales conditions d’application :

  1. Les résidus sont normalement distribués,
  2. La variance des résidus est égale dans tous les traitements (homoscédasticité) et
  3. Les résidus sont indépendants les uns des autres.

Ces conditions doivent être remplies avant que l’on puisse se fier aux résultats de l’ANOVA paramétrique.

  • Faites une ANOVA à un critère de classification sur la longueur (fklngth) par année (year) et produisez les graphiques diagnostiques
# Ajustez le modèle anova et affichez les graphiques diagnostiques des résidus
anova.model1 <- lm(fklngth ~ year, data = Dam10dat)
par(mfrow = c(2, 2))
plot(anova.model1)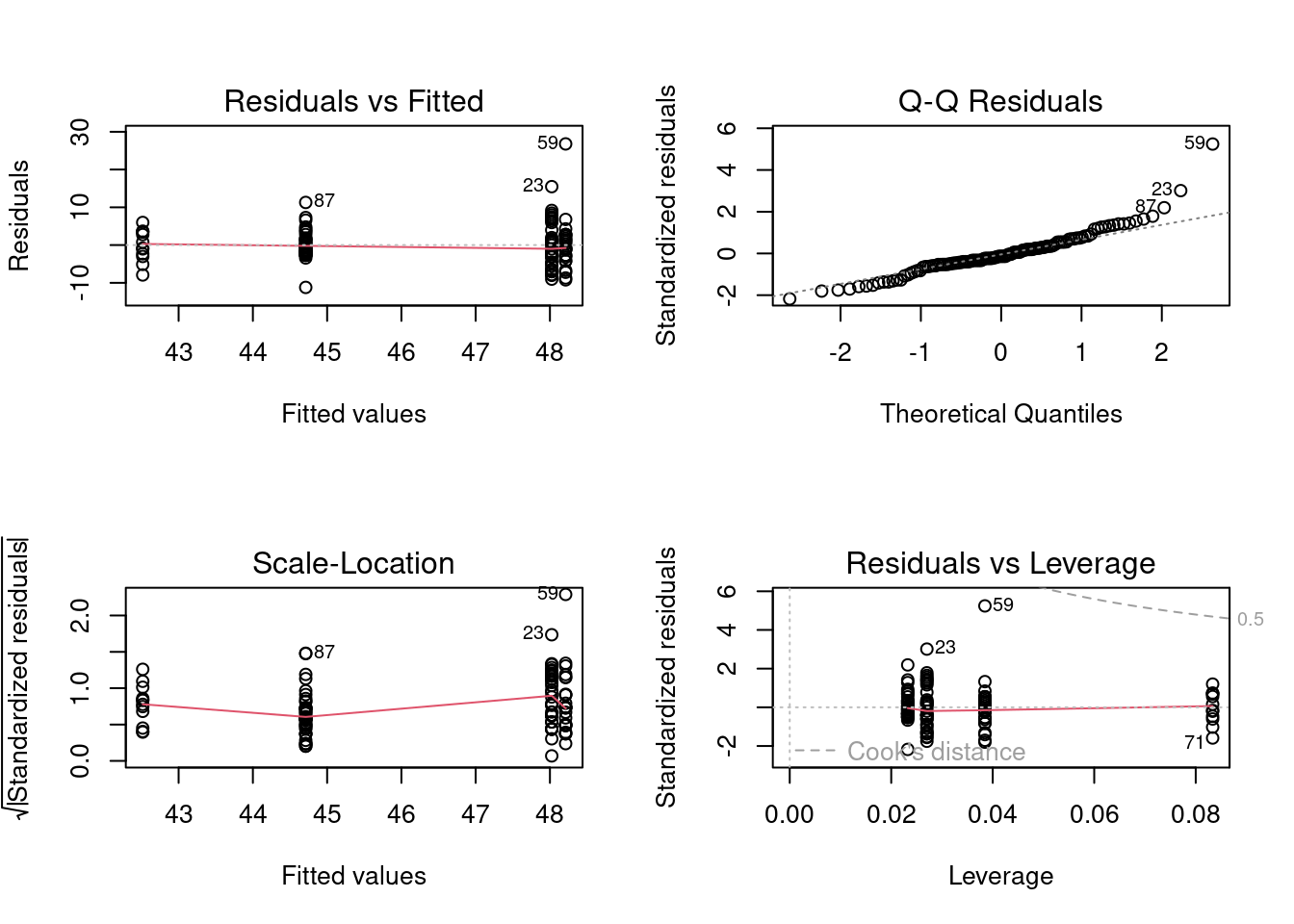
Figure 11.3: Conditions d’applications de l’ANOVA.
Avertissement

Vérifiez que la variable indépendant est bien un facteur. Si la variable indépendante est reconnu comme du texte (character) alors vous n’obtiendrez que 3 graphiques et un message d’erreur du type:

`hat values (leverages) are all = 0.1

and there are no factor predictors; no plot no. 5`

D’après les graphiques, on peut douter de la normalité et de l’homogénéité des variances. Notez qu’il y a un point qui ressort vraiment avec une forte valeur résiduelle (cas numéro 59) et qui ne s’aligne pas bien avec les autres valeurs : c’est la valeur extrême qui avait été détectée plus tôt. Ce point fera sans doute gonfler la variance résiduelle du groupe auquel il appartient.

Des tests formels nous aideront à confirmer ou infirmer les conclusions faites à partir de ces graphiques.

  • Test de normalité sur les résidus de l’ANOVA.
shapiro.test(residuals(anova.model1))

    Shapiro-Wilk normality test

data:  residuals(anova.model1)
W = 0.91571, p-value = 1.63e-06

Ce test confirme nos soupçons: les résidus ne sont pas distribués normalement. Il faut cependant garder à l’esprit que la puissance est grande et que même de petites déviations de la normalité sont suffisantes pour rejeter l’hypothèse nulle.

  • Test de l’hypothèse d’égalité des variances (homoscedasticité):
leveneTest(fklngth ~ year, data = Dam10dat)
Levene's Test for Homogeneity of Variance (center = median)
       Df F value  Pr(>F)  
group   3  2.8159 0.04234 *
      114                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La valeur de p vous dit que vous pouvez rejeter l’hypothèse nulle qu’il n’y a aucune différence dans les variances entre les années. Alors, nous concluons que les variances ne sont pas homogènes.

11.2.3 Faire l’ANOVA

  • Faites une ANOVA de fklnght en choisissant / présumant pour l’instant que les conditions d’application sont suffisamment remplies. Que concluez-vous?
summary(anova.model1)

Call:
lm(formula = fklngth ~ year, data = Dam10dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-11.2116  -2.6866  -0.7116   2.2103  26.7885 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  48.0243     0.8566  56.061  < 2e-16 ***
year1958      0.1872     1.3335   0.140  0.88859    
year1965     -5.5077     1.7310  -3.182  0.00189 ** 
year1966     -3.3127     1.1684  -2.835  0.00542 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.211 on 114 degrees of freedom
Multiple R-squared:  0.1355,    Adjusted R-squared:  0.1128 
F-statistic: 5.957 on 3 and 114 DF,  p-value: 0.0008246
  • Coefficients: Estimates: Les 4 coefficients peuvent être utilisés pour obtenir les valeurs prédites par le modèle (i.e., les moyennes de chaque groupe). La longueur à la fourche (fklngth) moyenne de la première année (1954) est \(48.0243\). Les coefficients pour les 3 autres années sont la différence entre la moyenne de l’année en question et la moyenne de 1954. La moyenne pour 1965 est \(48.0243-5.5077=42.5166\). Pour chaque coefficient, on a également accès à l’erreur-type, une valeur de t et la probabilité qui lui est associée (pour H0 que le coefficient est 0). Les poissons étaient plus petits après la construction du barrage qu’en 1954. Il faut néanmoins prendre ces p-valeurs avec un grain de sel, car elles ne sont pas corrigées pour les comparaisons multiples et elles ne constituent qu’un sous-ensemble des comparaisons possibles. En général, je porte peu d’attention à cette partie des résultats imprimés et me concentre sur ce qui suit.
  • Residual standard error: La racine carrée de la variance des résidus (valeurs observées moins valeurs prédites) qui correspond à la variabilité inexpliquée par le modèle (variation de la taille des poissons capturés la même année).
  • Mutiple R-squared: Le R-carré est la proportion de la variabilité de la variable dépendante qui peut être expliquée par le modèle. Ici, le modèle explique \(13.5\)% de la variabilité. Les différences de taille d’une année à l’autre sont relativement petites lorsqu’on les compare à la variation de taille entre les poissons capturés la même année.
  • F-Statistic: La p-valeur associée au test “omnibus” que toutes les moyennes sont égales. Ici, p est beaucoup plus petit que 0.05 et on rejetterait H0 pour conclure que fklngth varie selon les années.

La fonction anova() produit le tableau d’ANOVA standard qui contient la plupart de ces informations :

anova(anova.model1)
Analysis of Variance Table

Response: fklngth
           Df  Sum Sq Mean Sq F value    Pr(>F)    
year        3  485.26 161.755  5.9574 0.0008246 ***
Residuals 114 3095.30  27.152                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La variabilité totale de fklngth, mesurée par la somme du carré des écarts (Sum sq) est partitionnée en ce qui peut être expliqué par l’année (\(485.26\)) et la variabilité résiduelle inexpliquée (\(3095.30\)). L’année explique bien \(\frac{485.26}{3095.30+485.26}=0.1355\) or 13.55% de la variabilité. Le carré moyen des résidus (Residual Mean Sq) correspond à leur variance.

11.2.4 Les comparaisons multiples

  • La fonction pairwise.t.test() peut être utilisée pour comparer des moyennes et ajuster (ou non) les probabilités pour le nombre de comparaisons en utilisant l’une des options pour l’argument p.adj :

Comparez toutes les moyennes sans ajuster les probabilités :

pairwise.t.test(Dam10dat$fklngth, Dam10dat$year,
  p.adj = "none"
)

    Pairwise comparisons using t tests with pooled SD 

data:  Dam10dat$fklngth and Dam10dat$year 

     1954   1958   1965  
1958 0.8886 -      -     
1965 0.0019 0.0022 -     
1966 0.0054 0.0079 0.1996

P value adjustment method: none

L’option "bonf" ajuste les p-valeurs avec la correction de Bonferroni. Ici, il y a 6 valeurs p calculées, et la correction de Bonferroni revient à simplement multiplier la p-valeur par 6 (sauf si le résultat est supérieur à 1. Si tel est le cas, la “p-value” ajustée est 1).

pairwise.t.test(Dam10dat$fklngth, Dam10dat$year,
  p.adj = "bonf"
)

    Pairwise comparisons using t tests with pooled SD 

data:  Dam10dat$fklngth and Dam10dat$year 

     1954  1958  1965 
1958 1.000 -     -    
1965 0.011 0.013 -    
1966 0.033 0.047 1.000

P value adjustment method: bonferroni

L’option "holm" correspond à la correction séquentielle de Bonferroni dans laquelle les p-valeurs sont ordonnées de (i=1) la plus faible à (N) la plus grande. La correction pour les p-valeurs est \(\boldsymbol{(N-i+1)}\). Ici, il y a \(N=6\) paires de moyennes qui sont comparées. La plus petite valeur de p non corrigée est 0.0019 pour 1954 vs 1965. La p-valeur corrigée est donc \(0.0019*(6-1+1)=0.011\). La seconde plus petite p-valeur est 0.0022. Sa p-valeur corrigée est \(0.0022*(6-2+1)=0.011\). Pour la p-valeur la plus élevée, la correction est \((N-N+1)=1\), donc la p-valeur corrigée est égale à la p-valeur brute.

pairwise.t.test(Dam10dat$fklngth, Dam10dat$year,
  p.adj = "holm"
)

    Pairwise comparisons using t tests with pooled SD 

data:  Dam10dat$fklngth and Dam10dat$year 

     1954  1958  1965 
1958 0.889 -     -    
1965 0.011 0.011 -    
1966 0.022 0.024 0.399

P value adjustment method: holm

L’option "fdr" sert à contrôler le “false discovery rate”.

pairwise.t.test(Dam10dat$fklngth, Dam10dat$year,
  p.adj = "fdr"
)

    Pairwise comparisons using t tests with pooled SD 

data:  Dam10dat$fklngth and Dam10dat$year 

     1954   1958   1965  
1958 0.8886 -      -     
1965 0.0066 0.0066 -     
1966 0.0108 0.0119 0.2395

P value adjustment method: fdr

Les quatre méthodes mènent ici à la même conclusion: les poissons sont plus gros après la construction du barrage et toutes les comparaisons entre les années 50 et 60 sont significatives alors que les différences entre 54 et 58 ou 65 et 66 ne le sont pas. La conclusion ne dépend pas du choix de méthode.

Dans d’autres situations, vous pourriez obtenir des résultats contradictoires. Alors, quelle méthode choisir ? Les p-valeurs qui ne sont pas corrigées sont certainement suspectes lorsqu’il y a plusieurs comparaisons. D’un autre coté, la correction de Bonferroni est conservatrice et le devient encore plus lorsqu’il y a de très nombreuses comparaisons. Des travaux récents suggèrent que la correction fdr est un bon compromis lorsqu’il y a beaucoup de comparaisons.

La méthode de Tukey est l’une des plus populaires et est facile à utiliser en R (notez cependant qu’il y a un petit bug qui se manifeste quand la variable indépendante peut ressembler à un nombre plutôt qu’un facteur, ce qui explique la petite pirouette avec paste0() dans le code pour ajouter la lettre m avant le premier chiffre):

Dam10dat$myyear <- as.factor(paste0("m", Dam10dat$year))
TukeyHSD(aov(fklngth ~ myyear, data = Dam10dat))
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = fklngth ~ myyear, data = Dam10dat)

$myyear
                  diff        lwr        upr     p adj
m1958-m1954  0.1872141  -3.289570  3.6639986 0.9990071
m1965-m1954 -5.5076577 -10.021034 -0.9942809 0.0100528
m1966-m1954 -3.3126964  -6.359223 -0.2661701 0.0274077
m1965-m1958 -5.6948718 -10.436304 -0.9534397 0.0116943
m1966-m1958 -3.4999106  -6.875104 -0.1247171 0.0390011
m1966-m1965  2.1949612  -2.240630  6.6305526 0.5710111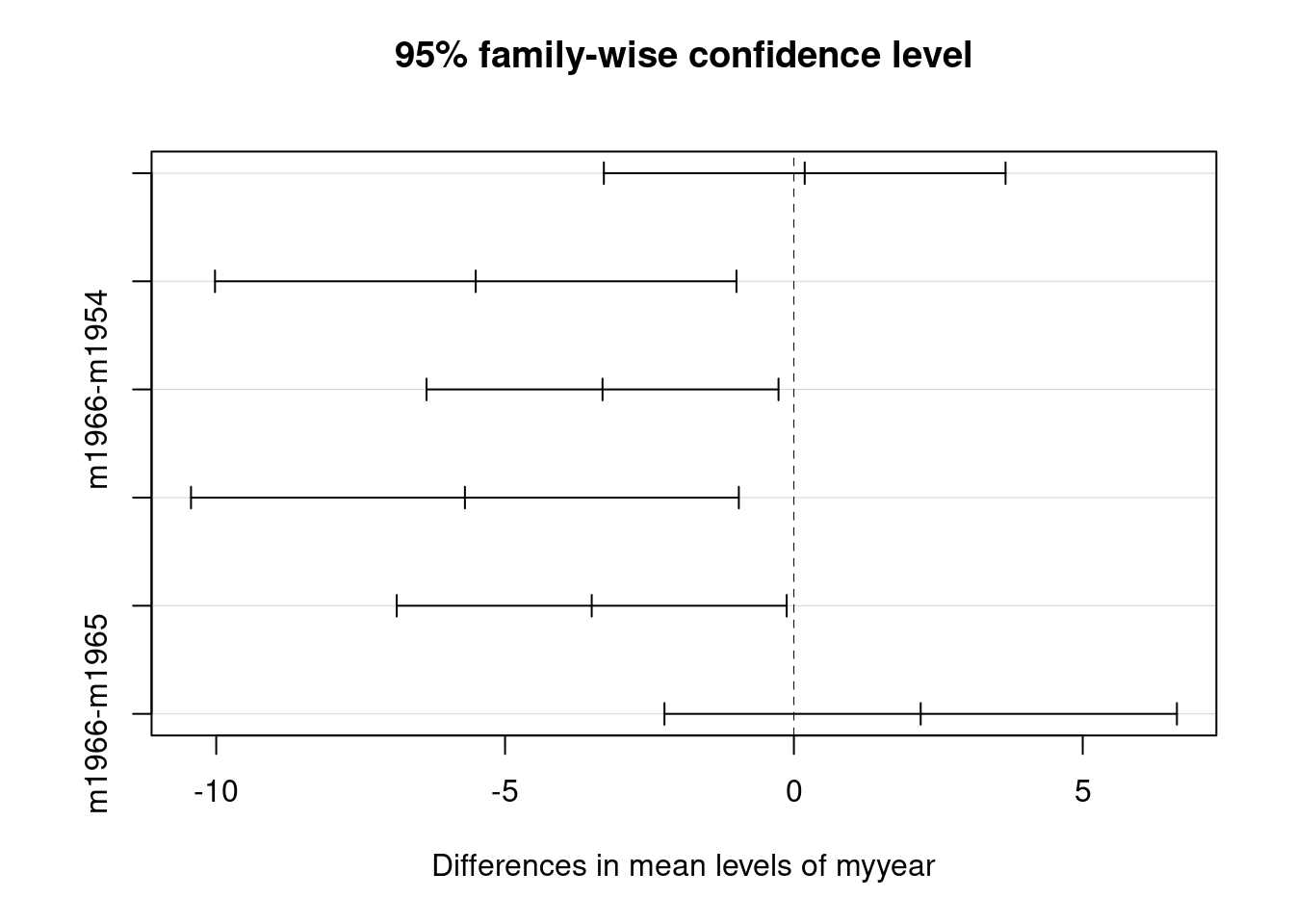
plot(TukeyHSD(aov(fklngth ~ myyear, data = Dam10dat)))
Figure 11.4: Différence anuelles dans la longueur des esturgeons.

Les intervalles de confiance, corrigés pour les comparaisons multiples par la méthode de Tukey, sont illustrés pour les différences entre années. Malheureusement les légendes ne sont pas complètes, mais l’ordre est le même que dans le tableau précédent.

Le paquet multcomp 📦 peut produire de meilleurs graphiques, mais requiert un peu plus de code:

# Autre manière de faire une comparaison multiple corrigée par la méthode de Tukey
# Ajustez une ANOVA à un critère de classification
anova.fkl.vs.year <- aov(aov(fklngth ~ myyear, data = Dam10dat))
# Établissez des comparaisons par paires pour le facteur `year`

meandiff <- glht(anova.fkl.vs.year, linfct = mcp(
  myyear =
    "Tukey"
))
confint(meandiff)

     Simultaneous Confidence Intervals

Multiple Comparisons of Means: Tukey Contrasts


Fit: aov(formula = aov(fklngth ~ myyear, data = Dam10dat))

Quantile = 2.5934
95% family-wise confidence level
 

Linear Hypotheses:
                   Estimate lwr      upr     
m1958 - m1954 == 0   0.1872  -3.2710   3.6454
m1965 - m1954 == 0  -5.5077  -9.9969  -1.0184
m1966 - m1954 == 0  -3.3127  -6.3429  -0.2825
m1965 - m1958 == 0  -5.6949 -10.4109  -0.9788
m1966 - m1958 == 0  -3.4999  -6.8571  -0.1428
m1966 - m1965 == 0   2.1950  -2.2169   6.6068
plot(meandiff)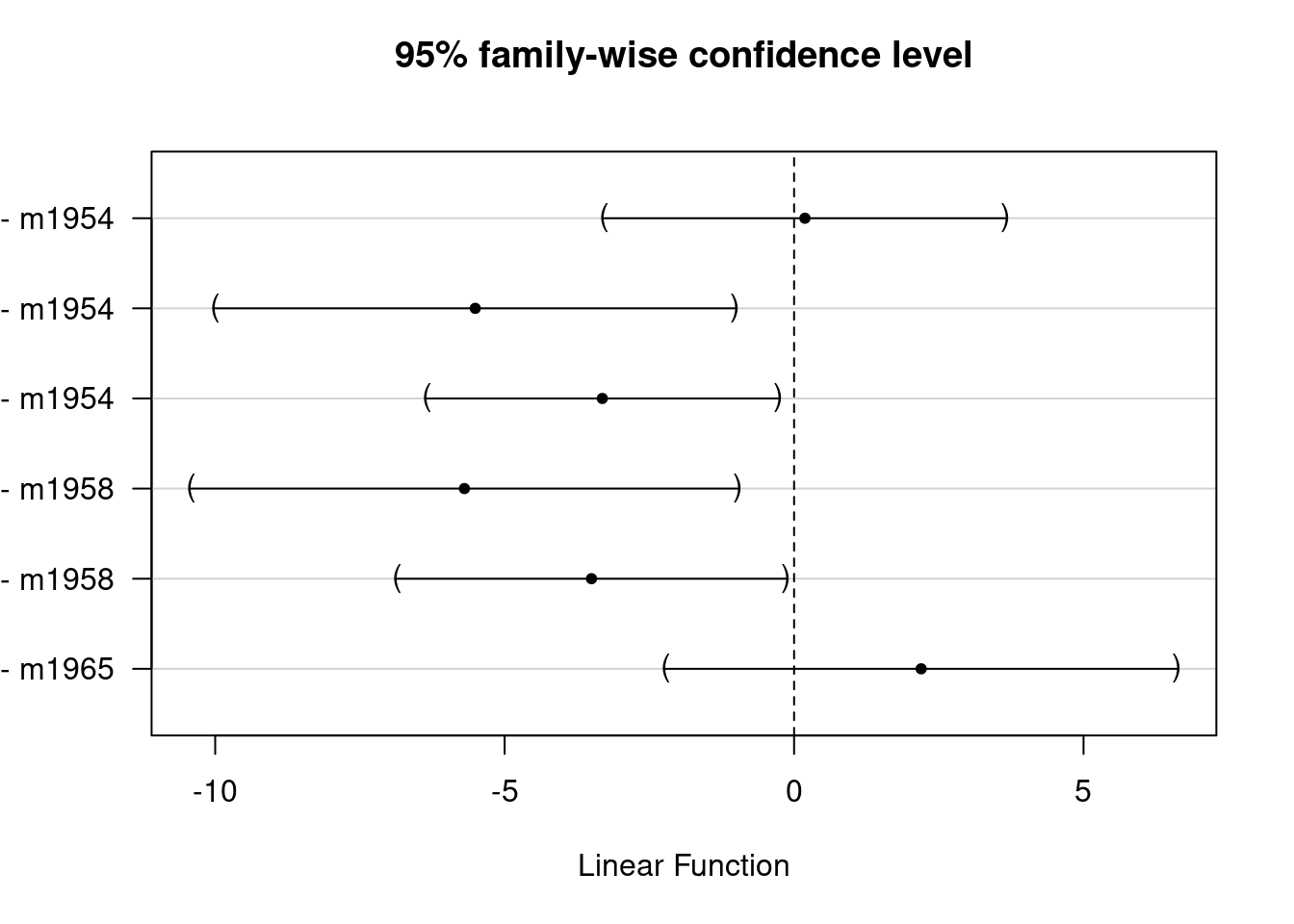
Figure 11.5: Différence anuelles dans la longueur des esturgeons (avec multcomp 📦).

C’est un peu mieux, mais ce qui le serait encore plus c’est un graphique des moyennes, avec leurs intervalles de confiance ajustés pour les comparaisons multiples:

# Calculez et représentez les moyennes et l'IC de Tukey
means <- glht(
  anova.fkl.vs.year,
  linfct = mcp(myyear = "Tukey")
)
cimeans <- cld(means)
# Utilisez une marge supérieure suffisamment grande
# Graphique
old.par <- par(mai = c(1, 1, 1.25, 1))
plot(cimeans)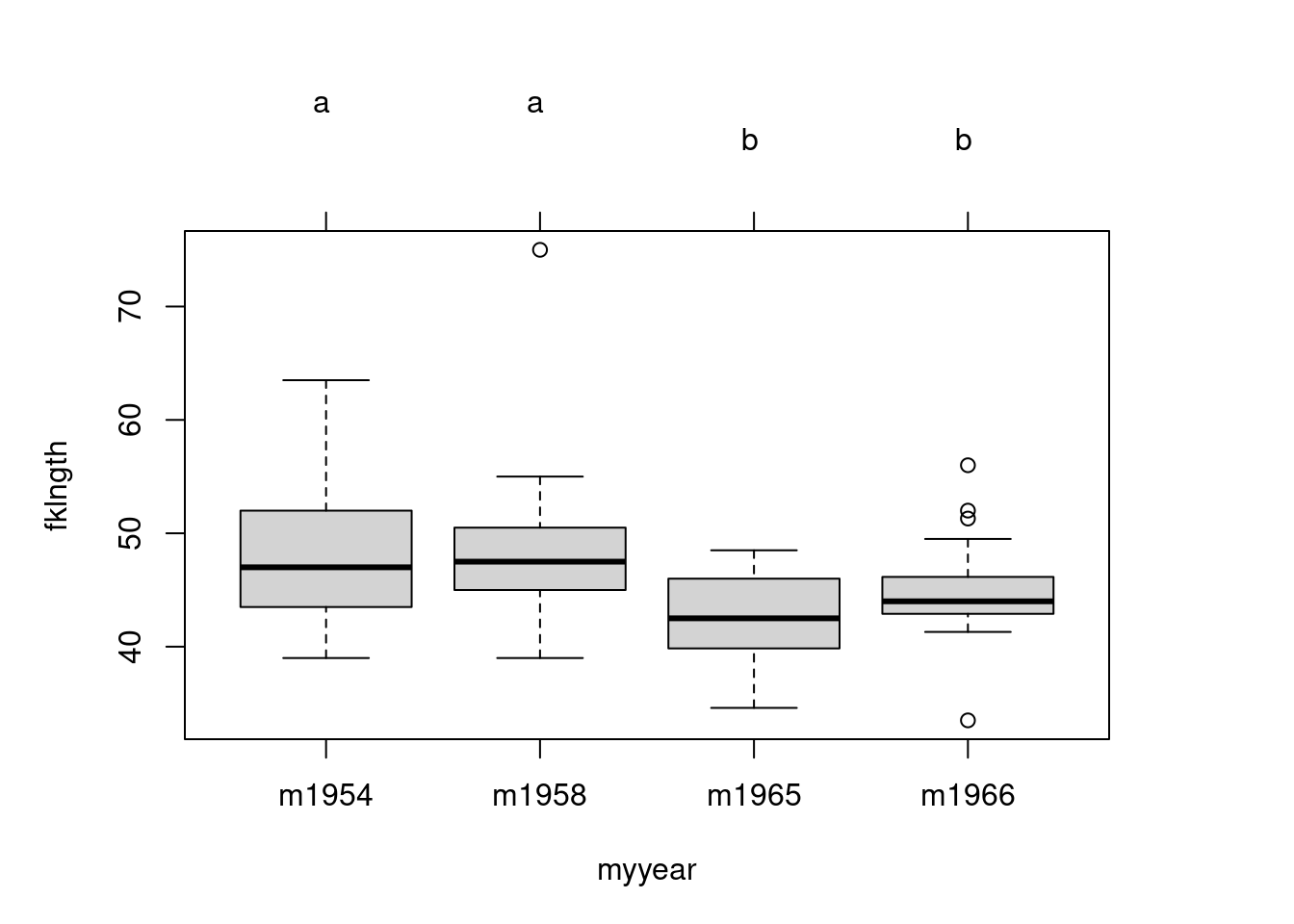
Figure 11.6: Différence anuelles dans la longueur des esturgeons.

Notez les lettres au dessus du graphique: les années étiquetées avec la même lettre ne diffèrent pas significativement l’une de l’autre.

11.3 Transformations de données et ANOVA non-paramétrique

Dans l’exemple précédent sur les différences annuelles de longueur (variable fklgnth), on a noté que les conditions d’application de l’ANOVA n’étaient pas remplies. Si les données ne remplissent pas les conditions de l’ANOVA paramétrique, il y a 3 options :

  1. Ne rien faire. Si les effectifs dans chaque groupe sont grands, on peut relaxer les conditions d’application car l’ANOVA est alors assez robuste aux violations de normalité (mais moins aux violations d’homoscedasticité),
  2. Transformer les données
  3. Faire une analyse non-paramétrique.
  • Refaites l’ANOVA de la section précédente après avoir transformé fglngth en logarithme de base 10. Avec les données transformées, est-ce que les problèmes qui avaient été identifiés disparaissent ?
# Ajustez un modèle anova avec une transformation log10 de `fklngth`et tracez les graphiques diagnostiques
par(mfrow = c(2, 2))
anova.model2 <- lm(log10(fklngth) ~ year, data = Dam10dat)
plot(anova.model2)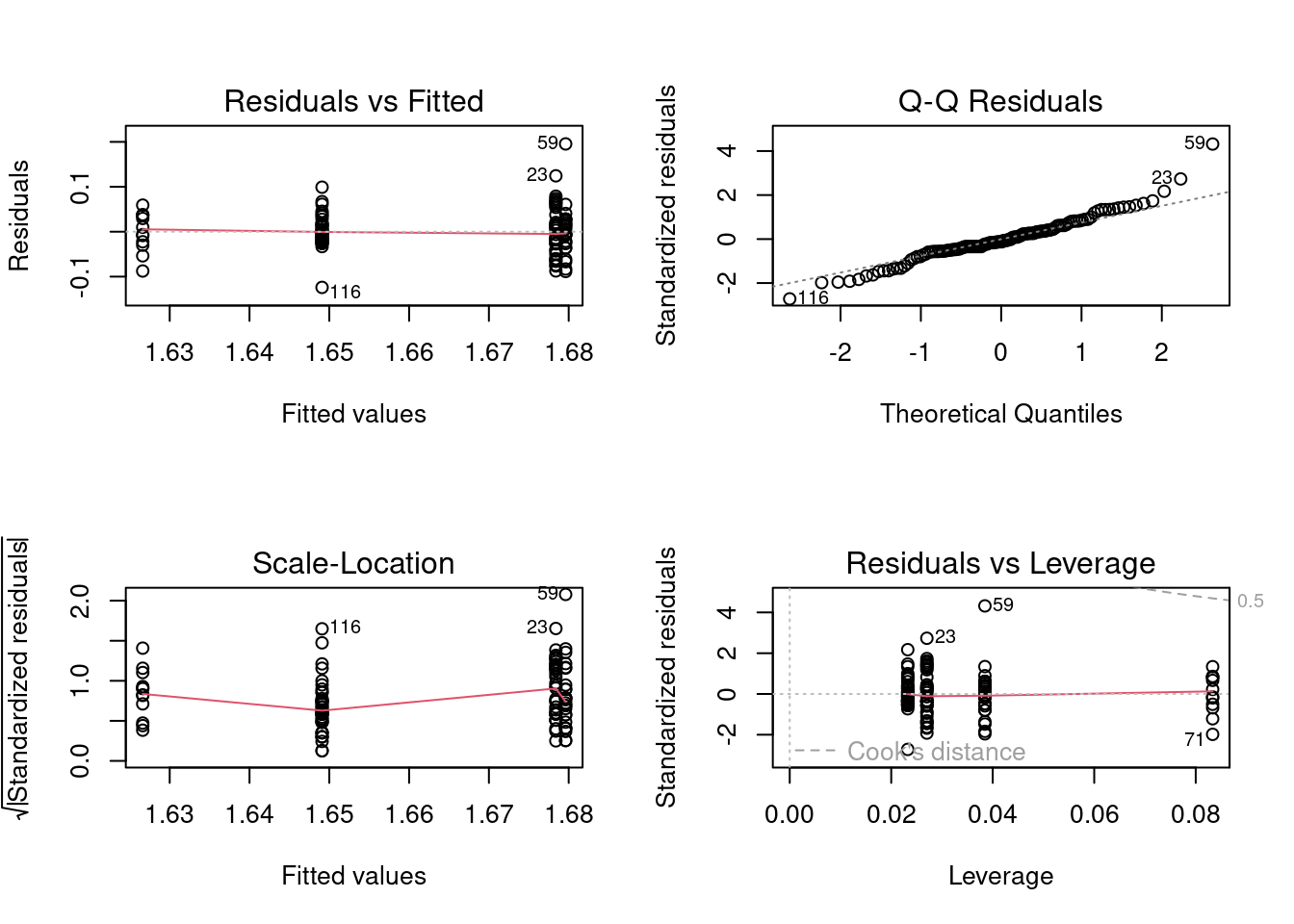
Figure 11.7: Conditions d’application de l’ANOVA.

Les graphiques sont à peine mieux ici. Si on fait le test Shapiro-Wilk sur les résidus, on obtient:

shapiro.test(residuals(anova.model2))

    Shapiro-Wilk normality test

data:  residuals(anova.model2)
W = 0.96199, p-value = 0.002048

Donc, on a toujours des problèmes avec la normalité et on est juste sur le seuil de décision pour l’égalité des variances. Vous avez le choix à ce point:

  1. Essayer de trouver une autre transformation pour mieux rencontrer les conditions d’application.
  2. Assumer que les données sont suffisamment proche des conditions d’application.
  3. Faire une ANOVA non-paramétrique.
  • L’analogue non-paramétrique de l’ANOVA à un critère de classification le plus employé est le test de Kruskall-Wallis. Faites ce test sur fklngth et comparez les résultats à ceux de l’analyse paramétrique. Que concluez-vous?
kruskal.test(fklngth ~ year, data = Dam10dat)

    Kruskal-Wallis rank sum test

data:  fklngth by year
Kruskal-Wallis chi-squared = 15.731, df = 3, p-value = 0.001288

La conclusion est donc la même qu’avec l’ANOVA paramétrique: on rejette l’hypothèse nulle que le rang moyen est le même pour chaque année. Donc, même si les conditions d’application de l’analyse paramétrique n’étaient pas parfaitement rencontrées, les conclusions sont les mêmes, ce qui illustre la robustesse de l’ANOVA paramétrique.

11.4 Examen des valeurs extrêmes

Vous devriez avoir remarqué au cours des analyses précédentes qu’il y avait peut-être des valeurs extrêmes dans les données. Ces points étaient évidents dans le “Box Plot” de fklngth par year et ont été notés comme les points 59, 23, et 87 dans les diagrammes de probabilité des résidus et dans le diagramme de dispersion des résidus et des valeurs estimées. En général, vous devez avoir de très bonnes raisons pour enlever des valeurs extrêmes de la base de données (i.e. vous savez qu’il y a eu une erreur avec un cas). Cependant, il est quand même toujours valable de voir comment l’analyse change en enlevant des valeurs extrêmes de la base de données.

  • Répétez l’ANOVA originale sur fklngth et year mais faites le avec un sous-ensemble de données sans les valeurs extrêmes. Est-ce que les conclusions ont changé?
Damsubset <- Dam10dat[-c(23, 59, 87), ] # enlevez les observations 23, 59 et 87
aov.Damsubset <- aov(fklngth ~ as.factor(year), Damsubset)
summary(aov.Damsubset)
                 Df Sum Sq Mean Sq F value   Pr(>F)    
as.factor(year)   3  367.5  122.50   6.894 0.000267 ***
Residuals       111 1972.4   17.77                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
shapiro.test(residuals(aov.Damsubset))

    Shapiro-Wilk normality test

data:  residuals(aov.Damsubset)
W = 0.98533, p-value = 0.2448
leveneTest(fklngth ~ year, Damsubset)
Levene's Test for Homogeneity of Variance (center = median)
       Df F value   Pr(>F)   
group   3  4.6237 0.004367 **
      111                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

L’élimination de trois valeurs extrêmes améliore un peu les choses, mais ce n’est pas parfait. On a toujours un problème avec les variances, mais les résidus sont maintenant normaux. Cependant, le fait que la conclusion qu’on tire de l’ANOVA originale ne change pas en enlevant les points renforce le fait qu’on n’a pas de raison valable pour enlever ces points.

11.5 Test de permutation

Commande R pour un test de permutation d’une ANOVA à un critère de classification.

#############################################################
# Test de permutation pour ANOVA à un critère de classification
# modifié à partir du code écrit par David C. Howell
# http://www.uvm.edu/~dhowell/StatPages/More_Stuff/Permutation%20Anova/PermTestsAnova.html
# Définition du nombre de permutation
nreps <- 500
# Pour simplifier la réutilisation de ce code, assignez le jeu de donnée à utiliser à l'objet "mydata"
mydata <- Dam10dat
# Stockez la formule de votre modèle dans l'objet myformula
myformula <- as.formula("fklngth ~ year")
# Stockez la variable dépendante dans l'objet mydep
mydep <- mydata$fklngth
# Stockez la variable indépendante dans l'objet myindep
myindep <- as.factor(mydata$year)
################################################

# Vous ne devriez pas avoir besoin de modifier le code ci-dessous

################################################
# Calculez la valeur F observée pour l'échantillon original
mod1 <- lm(myformula, data = mydata) # Anova Standard
ANOVA <- summary(aov(mod1)) # Stockez le résumé dans une variable
observedF <- ANOVA[[1]]$"F value"[1] # Stockez la valeur F observée
# Affichez les résultats de l'ANOVA standard
cat(
  " L'ANOVA standard pour ces données est la suivante ",
  "\n"
)

print(ANOVA, "\n")
cat("\n")
cat("\n")
print("Rééchantillonnage comme dans Manly avec échantillonnage non restreint des observations. ")

# Commençons le rééchantillonnage
Fboot <- numeric(nreps) # initialisez le vecteur pour qu'il soit permuté
values
Fboot[1] <- observedF
for (i in 2:nreps) {
  newdependent <- sample(mydep, length(mydep)) # Randomiser la variable dépendante
  var
  mod2 <- lm(newdependent ~ myindep) # Réajuste le modèle
  b <- summary(aov(mod2))
  Fboot[i] <- b[[1]]$"F value"[1] # Stock la statistique F
}
permprob <- length(Fboot[Fboot >= observedF]) / nreps
cat(
  " The permutation probability value is: ", permprob,
  "\n"
)
# Fin du bloc de code de permutation.

Version lmPerm du test de permutation :

## Version lmPerm du test de permutation
library(lmPerm)
# Pour généraliser, assignez votre jeu de donnée à l'objet mydata
# et la formule du modèle à myformula
mydata <- Dam10dat
myformula <- as.formula("fklngth ~ year")
# Ajustez le modèle souhaité sur le jeu de donnée souhaité
mymodel <- lm(myformula, data = mydata)
# Calcule de la valeur p permuté
anova(lmp(myformula, data = mydata, perm = "Prob", center = FALSE, Ca = 0.001))