9  Corrélation et régression linéaire simple

Objectifs de ce chapitre :

9.1 Paquets R et données requises

Pour ce laboratoire vous aurez besoin de :

  • paquets R :
    • car 📦
    • lmtest 📦
    • boot 📦
    • pwr 📦
    • ggplot 📦
  • Jeu de données :
    • “sturgeon.csv”

Il ne faut pas oublier de charge les paquets avec library() (et de les installer au besoin avec install.packages()). Pour les données, il faut les charger et les assigner à un objet R avec la fonction read.csv().

library(car)
library(lmtest)
library(boot)
library(ggplot2)
library(pwr)
library(performance)

esturgeon <- read.csv("data/sturgeon.csv")
Note

Notez que la ligne de code pour charger les données considère que le fichier de données se trouve dans un dossier data au sein de votre répertoire de travail. Si ce n’est pas le cas veuillez ajuster la ligne de commande selon votre répertoire de travail.

9.2 Diagrammes de dispersion

Les analyses de corrélation et de régression devraient toujours commencer par un examen des données; c’est une étape critique qui sert à évaluer si ce type d’analyse est approprié pour un ensemble de données. Supposons que nous voulons évaluer si la longueur d’esturgeons mâles dans la région de The Pas covarie avec leur poids. Pour répondre à cette question, regardons d’abord la corrélation entre la longueur et le poids. Souvenez-vous qu’une des conditions d’application de l’analyse de corrélation est que la relation entre les deux variables est linéaire. Pour évaluer cela, commençons par faire un diagramme de dispersion.

  • Les données sur les esturgeons son disponibles dans le fichier sturgeon.csv. Après avoir chargé les données en les assignant à un objet esturgeon, faites un diagramme de dispersion avec une droite de régression linéaire et une courbe de Lowess de la longueur en fonction du poids.
esturgeon <- read.csv("data/sturgeon.csv")
str(esturgeon)
'data.frame':   186 obs. of  9 variables:
 $ fklngth : num  37 50.2 28.9 50.2 45.6 ...
 $ totlngth: num  40.7 54.1 31.3 53.1 49.5 ...
 $ drlngth : num  23.6 31.5 17.3 32.3 32.1 ...
 $ rdwght  : num  15.95 NA 6.49 NA 29.92 ...
 $ age     : int  11 24 7 23 20 23 20 7 23 19 ...
 $ girth   : num  40.5 53.5 31 52.5 50 54.2 48 28.5 44 39 ...
 $ sex     : chr  "MALE" "FEMALE" "MALE" "FEMALE" ...
 $ location: chr  "THE_PAS" "THE_PAS" "THE_PAS" "THE_PAS" ...
 $ year    : int  1978 1978 1978 1978 1978 1978 1978 1978 1978 1978 ...
mongraph <- ggplot(
  data = esturgeon[!is.na(esturgeon$rdwght), ], # origine des données
  aes(x = fklngth, y = rdwght)
)
# Représentez les données sous forme de Points, Régression linéaire, "Lowess"
mongraph <- mongraph +
  geom_smooth(method = lm, se = FALSE, color = "green") + # Ajoutez une régression linéaire, mais sans l'erreur-type (en vert)
  geom_smooth(color = "red", se = FALSE) + # Ajoutez la "lowess" (en rouge)
  geom_point() + # Ajoutez les données sous forme de points
  labs(x = "Longueur", y = "Poids") # Modifiez les noms des axes pour rendre le graphique plus lisible

mongraph # Affichez le graphique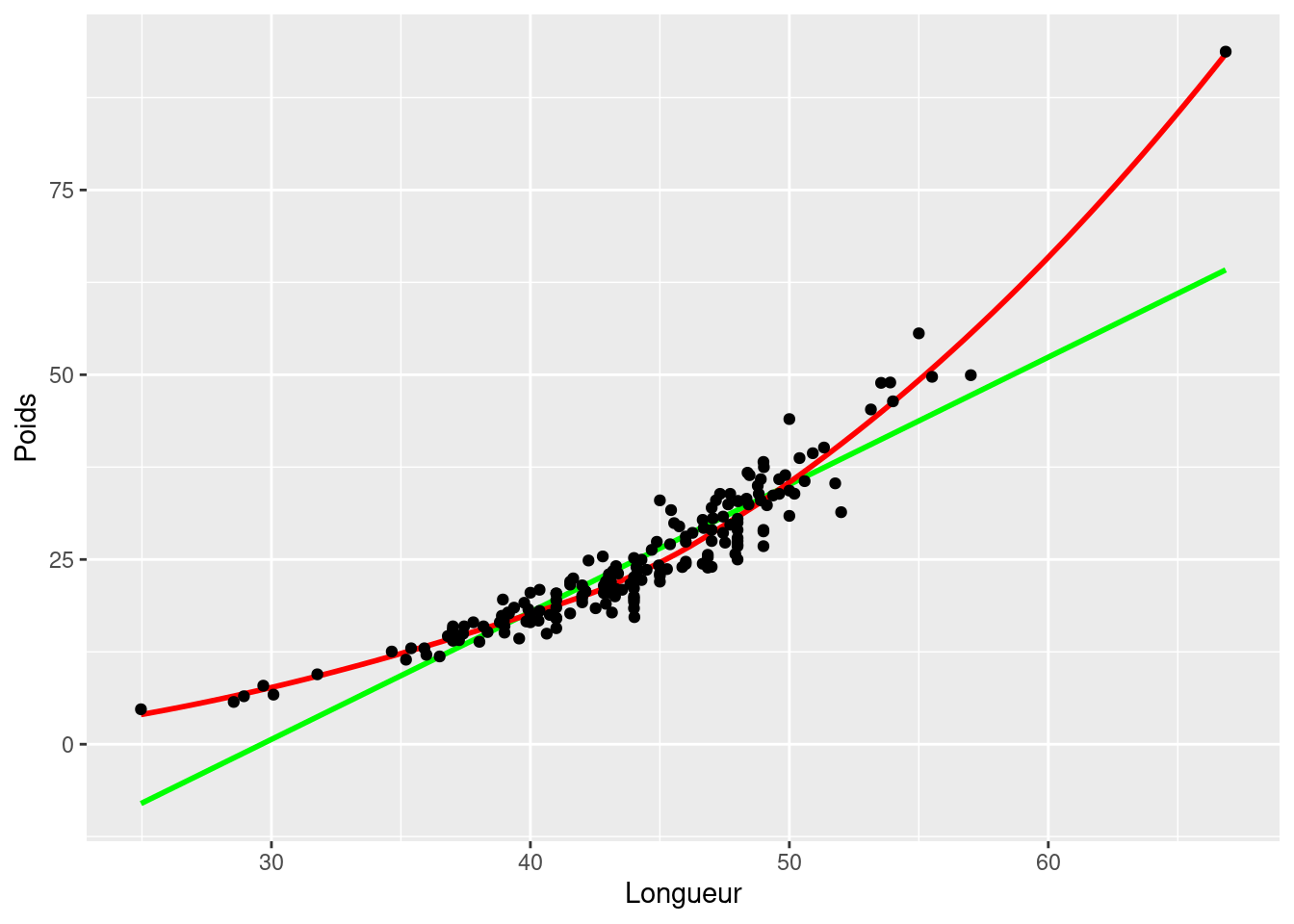
Figure 9.1: Graphique du poids en fonction de la longueur des esturgeons.
  • Est-ce que la dispersion des points suggère une bonne corrélation entre les deux variables? Est-ce que la relation semble linéaire?

Ce graphique suggère une tendance plus curvilinéaire que linéaire. Malgré tout, il semble y avoir une forte corrélation entre les deux variables.

  • Refaites le diagramme de dispersion avec des transformations logarithmiques sur les deux axes.
# Appliquez une transformation log sur le graphique déjà défini
mongraph + scale_x_log10() + scale_y_log10()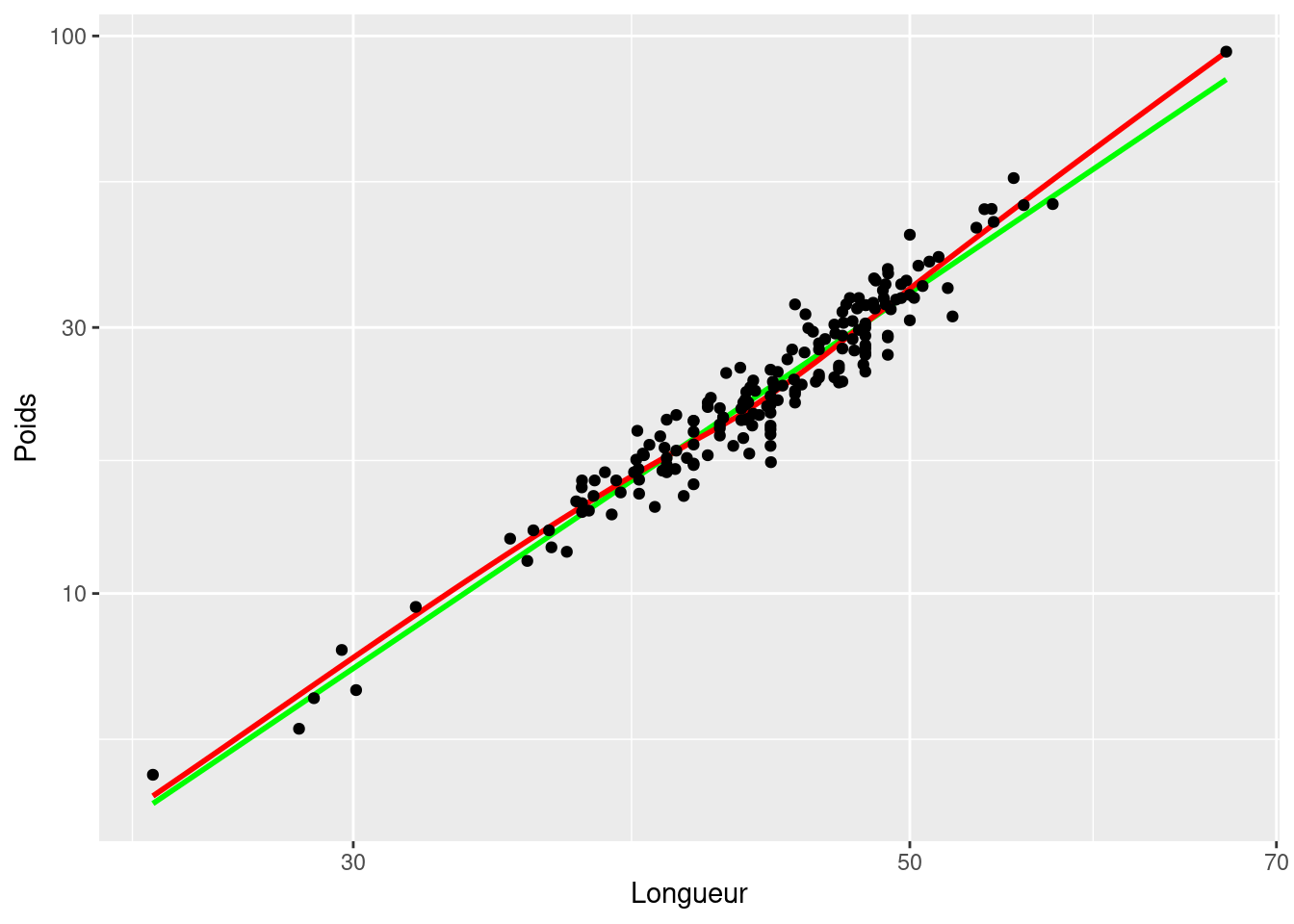
Figure 9.2: Graphique poids-longueur avec une échelle log.

Comparez les diagrammes de dispersion avant et après transformation (Figure 9.1 et Figure 9.2). Sachant que l’analyse de corrélation présuppose une relation linéaire entre les variables, on devrait donc privilégier l’analyse sur les données log-transformées.

9.3 Transformations de données et coefficient de corrélation

Une autre condition préalable à l’analyse de corrélation est que les deux variables concernées suivent une distribution normale bivariée. On peut aisément vérifier la normalité de chacune des 2 variables séparément tel que décrit dans plus bas dans la section Section 9.6.1. Si les deux variables sont normalement distribuées, on présume généralement que la distribution commune des deux variables est également normale (notez que ce n’est pas toujours le cas cependant).

  • Examinez la distribution des quatre variables (les deux variables originales et les variables transformées). Que concluez-vous de l’inspection visuelle de ces graphiques ?

Les figures ci-dessous sont les 4 diagrammes Q(uantile)-Q(uantile) (qqplot()). Le code pour produire des graphiques multiples sur une seule page avec 2 lignes et 2 colonnes, comme on voit ci-dessous, est :

par(mfrow = c(2, 2)) # divise le graphique en 4 sections
qqnorm(esturgeon$fklngth, ylab = "fklngth")
qqline(esturgeon$fklngth)
qqnorm(log10(esturgeon$fklngth), ylab = "log10(fklngth)")
qqline(log10(esturgeon$fklngth))
qqnorm(esturgeon$rdwght, ylab = "rdwght")
qqline(esturgeon$rdwght)
qqnorm(log10(esturgeon$rdwght), ylab = "log10(rdwgth)")
qqline(log10(esturgeon$rdwght))
par(mfrow = c(1, 1)) # redéfinie la zone de graphique par défaut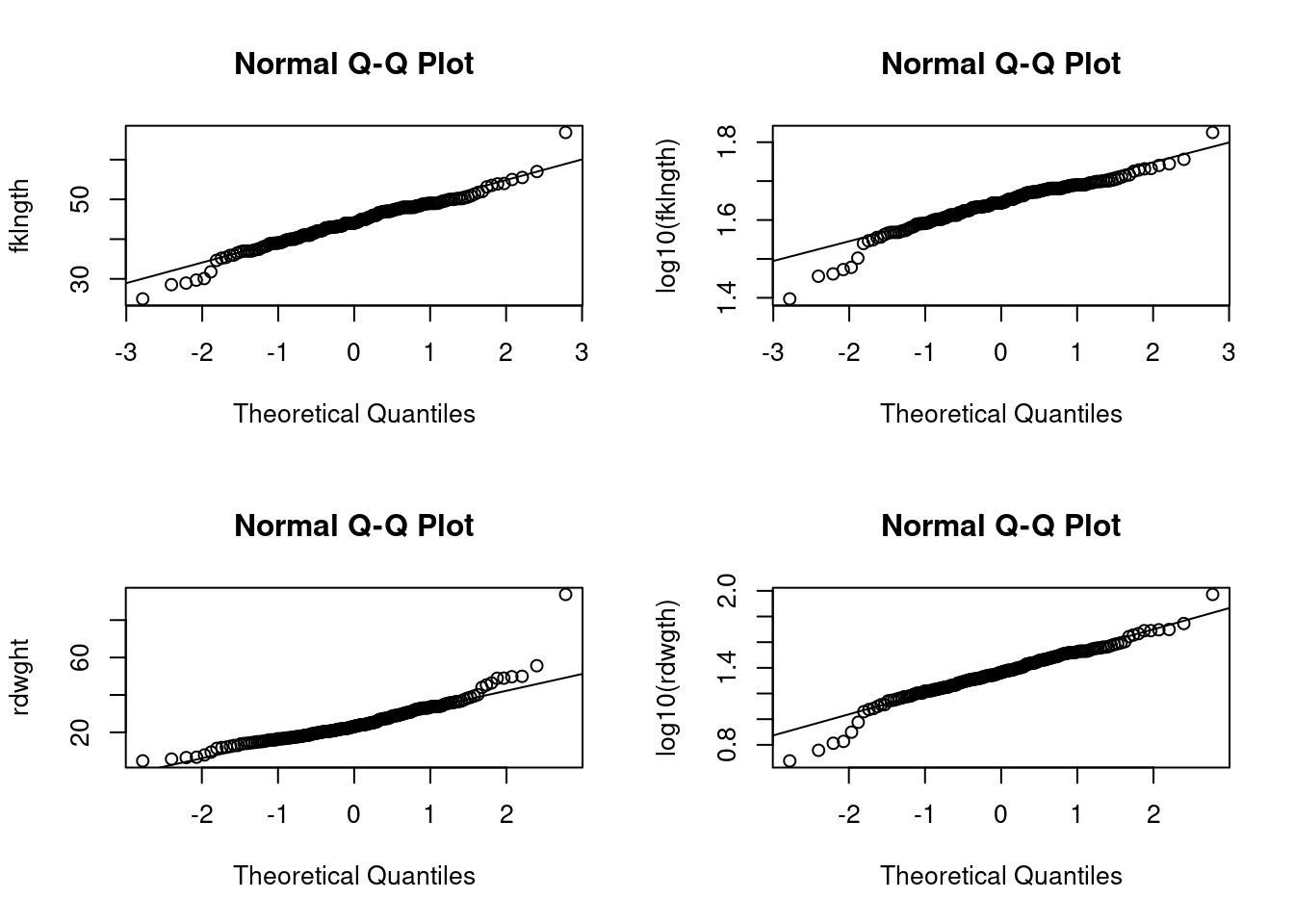
Figure 9.3: Diagrammes Q-Q des quatres variables étudiées (Poids, Longueur, Originale et Log-transformées).

Il n’y a pas grand-chose à redire: aucune des distributions n’est parfaitement normale, mais les déviations semblent mineures.

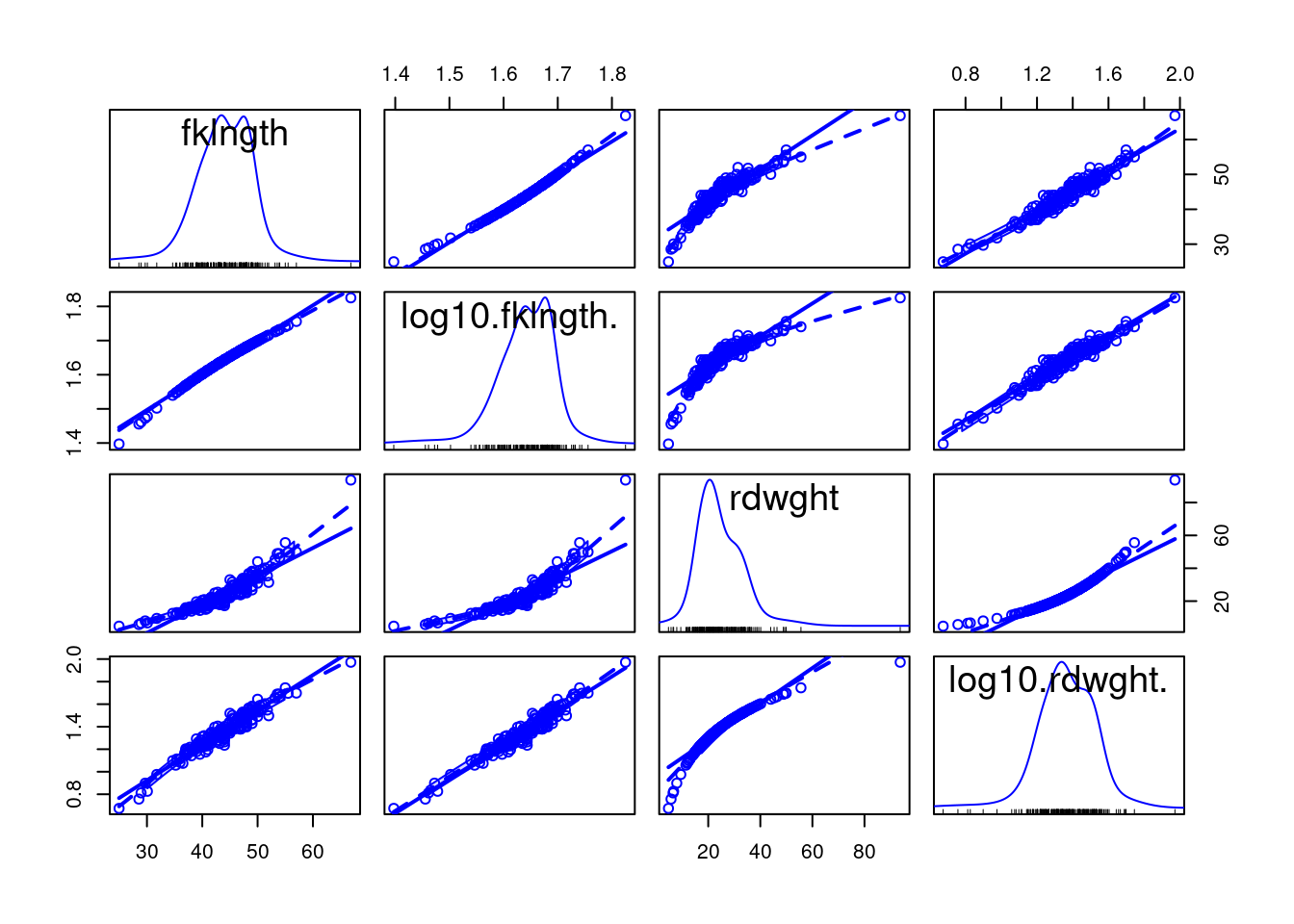
  • Générez une matrice de graphiques de dispersion de toutes les paires de variables (avec régression linéaires et “lowess”) en utilisant la fonction scatterplotMatrix du paquet car 📦.
scatterplotMatrix(
  ~ fklngth + log10(fklngth) + rdwght + log10(rdwght),
  data = esturgeon,
  smooth = TRUE, diagonal = "density"
)
Figure 9.4: Corrélations entre chaque paires de variables
  • Ensuite, calculez le coefficient de corrélation de Pearson entre chaque paire (variables originales et log-transformées) en utilisant la fonction cor(). Avant de commencer, on va cependant ajouter les variables transformées au jeu de données esturgeon :
esturgeon$lfklngth <- with(esturgeon, log10(fklngth))
esturgeon$lrdwght <- log10(esturgeon$rdwght)

Vous pouvez ensuite obtenir la matrice de corrélation par :

cor(esturgeon[, c("fklngth", "lfklngth", "lrdwght", "rdwght")], use = "complete.obs")

Fréquemment, il y a des données manquantes dans un échantillon. En précisant use="complete.obs", toutes les lignes du fichier pour lesquelles les variables ne sont pas toutes mesurées sont éliminées. Dans ce cas, toutes les corrélations seront calculées avec le même nombre de cas. Par contre, en utilisant use="pairwise.complete.obs", R élimine une observation seulement lorsque l’un des deux membres de la paire a une valeur manquante. Dans ce cas, si les données manquantes pour différentes variables se retrouvent dans un groupe différent d’observation, les corrélations ne seront pas nécessairement calculées sur le même nombre de cas ni sur le même sous-ensemble de cas. En général, vous devriez utiliser l’option use="complete.obs" à moins que vous ayez un très grand nombre de données manquantes et que cette façon de procéder élimine la plus grande partie de vos observations.

Pourquoi la corrélation entre les variables originales est-elle plus faible qu’entre les variables transformées ?

cor(esturgeon[, c("fklngth", "lfklngth", "lrdwght", "rdwght")], use = "complete.obs")
           fklngth  lfklngth   lrdwght    rdwght
fklngth  1.0000000 0.9921435 0.9645108 0.9175435
lfklngth 0.9921435 1.0000000 0.9670139 0.8756203
lrdwght  0.9645108 0.9670139 1.0000000 0.9265513
rdwght   0.9175435 0.8756203 0.9265513 1.0000000

Il y a plusieurs choses à noter ici.

  • Premièrement, la corrélation entre la longueur (“fklngth”) et le poids (“rdwght”) est élevée, peu importe la transformation: les poissons lourds ont tendance à être longs.
  • Deuxièmement, la corrélation est plus forte pour les données transformées que pour les données brutes.

Pourquoi? Parce que le coefficient de corrélation est inversement proportionnel au bruit autour de la relation linéaire. Si la relation est curvilinéaire (comme dans le cas des données non transformées), le bruit est plus grand que si la relation est parfaitement linéaire. Par conséquent, la corrélation est plus faible.

9.4 Matrices de corrélations et correction de Bonferroni

Une pratique courante est d’examiner la matrice de corrélation à la recherche d’associations significatives. Comme exemple, essayons de tester si la corrélation entre lfklngth et rdwght est significative (le plus faible coefficient de corrélation de cette matrice).

  • Estimez la corrélation entre la longueur (fklngth et le poids (rdwght) des esturgeons:
cor.test(
  esturgeon$lfklngth, esturgeon$rdwght,
  alternative = "two.sided",
  method = "pearson"
)

    Pearson's product-moment correlation

data:  esturgeon$lfklngth and esturgeon$rdwght
t = 24.322, df = 180, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.8367345 0.9057199
sample estimates:
      cor 
0.8756203

On voit ici que la corrélation est hautement significative (\(p < 2.2e-16\)), ce qui n’est pas surprenant étant donné la valeur du coefficient de corrélation (0.8756 = 87.6%). Il est important de réaliser que si une matrice contient un grand nombre de corrélations, il n’est pas surprenant d’en trouver au moins une qui soit “significative”. En effet, on s’attend à en trouver 5% en moyenne lorsqu’il n’y a en fait aucune corrélation entre les paires de moyennes (correspondant au risque d’erreur de type I \(\alpha\)) . Une façon de corriger pour cette tendance est d’ajuster le niveau \(\alpha\) critique auquel on attribue une signification statistique en divisant \(\alpha\) par le nombre \(k\) de corrélations qui sont examinées :

\(\alpha' = \alpha / k\) (ajustement de Bonferroni).

Si initialement \(\alpha = 0.05\) et qu’il y a 10 corrélations qui sont examinées, alors \(\alpha'= 0.005\). Donc, afin de rejeter l’hypothèse nulle, la valeur de p devra être plus petite que \(\alpha'\), en l’occurrence 0.005. Dans l’exemple qui précède, on devrait donc ajuster \(\alpha\) critique en divisant par le nombre total de corrélations dans la matrice (6 dans ce cas, donc \(\alpha'=0.00833\)). Cette correction modifie-t-elle votre conclusion quant à la corrélation entre lkflngth et rdwght?

9.5 Corrélations non paramétriques: r de Spearman et \(\tau\) de Kendall

L’analyse faite dans la section précédente avec les esturgeons suggère que l’une des conditions préalables à l’analyse de corrélation, soit la distribution normale bivariée de données, pourrait ne pas être remplie pour fklngth et rdwght, ni pour les paires de variables transformées. La recherche d’une transformation appropriée peut parfois être difficile. Pire encore, pour certaines distributions il n’existe pas de transformation qui va normaliser les données. Dans ces cas-là, la meilleure option est de faire une analyse non paramétrique qui ne présume ni de la normalité ni de la linéarité. Ces analyses sont basées sur les rangs. Les deux plus communes sont le coefficient de rang de Spearman et le \(\tau\) (tau) de Kendall.

  • Dans R, testez la corrélation entre fklngth et rdwght en utilisant Spearman et Kendall’s .
cor.test(
  esturgeon$lfklngth, esturgeon$rdwght,
  alternative = "two.sided",
  method = "spearman"
)
Warning in cor.test.default(esturgeon$lfklngth, esturgeon$rdwght, alternative =
"two.sided", : Cannot compute exact p-value with ties

    Spearman's rank correlation rho

data:  esturgeon$lfklngth and esturgeon$rdwght
S = 47971, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.9522546 
cor.test(
  esturgeon$lfklngth, esturgeon$rdwght,
  alternative = "two.sided",
  method = "kendall"
)

    Kendall's rank correlation tau

data:  esturgeon$lfklngth and esturgeon$rdwght
z = 16.358, p-value < 2.2e-16
alternative hypothesis: true tau is not equal to 0
sample estimates:
      tau 
0.8208065

Comparer les résultats de cette analyse à l’analyse paramétrique. Pourquoi y-a-t’il une différence ?

Calculez les corrélations non paramétriques sur les paires de variables transformées. Vous devriez voir tout de suite que les corrélations des données transformées et non transformées sont identiques puisque dans les deux cas la corrélation est calculée à partir des rangs qui ne sont pas affectés par la transformation.

Notez que les corrélations obtenues avec le \(\tau\) de Kendall (0.820) sont plus faibles que celles du coefficient de Spearman (0.952). Le \(\tau\) de Kendall pondère un peu plus les grandes différences entre les rangs alors que le coefficient de Spearman donne le même poids à chaque paire d’observations. En général, on préfère le \(\tau\) de Kendall lorsqu’il y a plus d’incertitude quant aux rangs qui sont près les uns des autres.

Les esturgeons de cet échantillon ont été capturés à l’aide de filets et d’hameçons d’une taille fixe. Quel impact cette méthode de capture peut-elle avoir eu sur la forme de la distribution de fklngth et rdwght? Compte tenu de ces circonstances, l’analyse de corrélation est-elle appropriée ?

Rappelez-vous que l’analyse de corrélation présume aussi que chaque variable est échantillonnée aléatoirement. Dans le cas de nos esturgeons, ce n’est pas le cas: les hameçons appâtés et les filets ne capturent pas de petits esturgeons (et c’est pourquoi il n’y en a pas dans l’échantillon). Il faut donc réaliser que les coefficients de corrélation obtenus dans cette analyse ne reflètent pas nécessairement ceux de la population totale des esturgeons.

9.6 Régression linéaire simple

L’analyse de corrélation vise à décrire comment deux variables covarient. L’analyse de régression vise plutôt à produire un modèle permettant de prédire une variable (la variable dépendante) par l’autre (la variable indépendante).

Comme pour l’analyse de corrélation, on devrait commencer en examinant des graphiques. Puisque l’on veut quantifier la relation entre deux variables, un graphique de la variable dépendante (Y) en fonction de la variable indépendante (X) est tout à fait approprié.

  • Le fichier sturgeon.csv contient les données d’un inventaire d’esturgeons récoltés entre 1978 et 1980 à Cumberland House en Saskatchewan et à The Pas au Manitoba. Faites un diagramme de dispersion de fklngth (la variable dépendante, Y) en fonction de l’age (la variable indépendante, X) pour les esturgeons mâles uniquement et ajoutez-y une régression linéaire et une “lowess”. Que concluez-vous de ce diagramme de dispersion ?
esturgeon.male <- subset(esturgeon, subset = sex == "MALE")
mongraph <- ggplot(
  data = esturgeon.male, # origine des données
  aes(x = age, y = fklngth)
) # aesthetics: y=fklngth, x=rdwght
# Représentez les données sous forme de Points, Régression linéaire, "Lowess"
mongraph <- mongraph +
  geom_smooth(method = lm, se = FALSE, color = "green") + # Ajoutez une régression linéaire, mais sans l'erreur-type (en vert)
  geom_smooth(color = "red") + # Ajoutez la "lowess" (en rouge)
  geom_point() +# Ajoutez les données sous forme de points
  labs(x = "Age", y = "Longueur") # Modifiez les noms des axes pour rendre le graphique plus lisible
mongraph # Affichez le graphique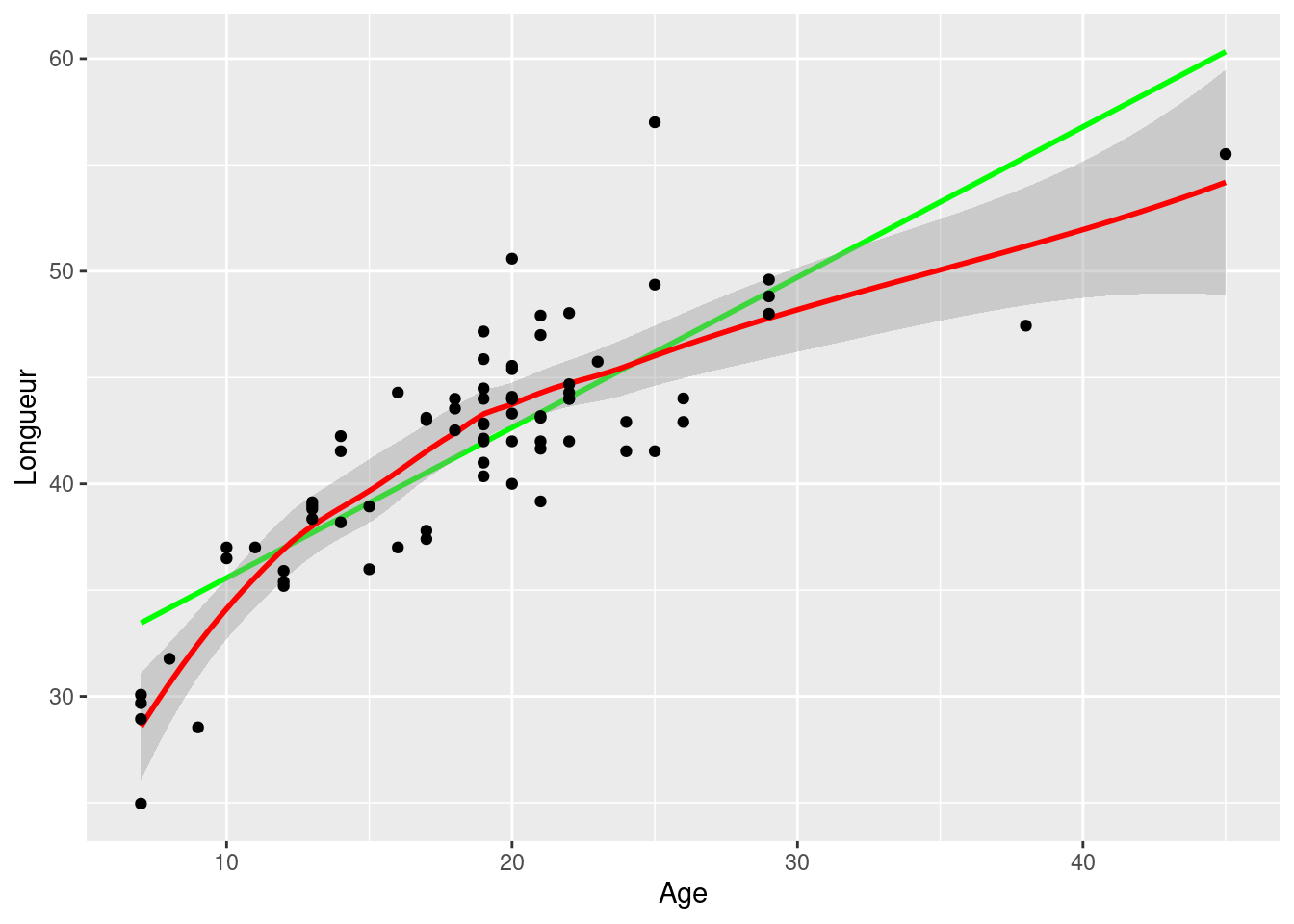
Figure 9.5: Graphique de la longueur en fonction de l’âge des esturgeons males.

Ce graphique suggère que la relation n’est pas linéaire.

Supposons que nous désirions estimer le taux de croissance des esturgeons mâles. Un estimé (peut-être pas terrible…) du taux de croissance peut être obtenu en calculant la pente de la régression de la longueur en fonction de l’âge.

Ajustons d’abord une régression avec la commande lm() et sauvons ces résultats dans un objet appelé RegModel.1.

RegModele.1 <- lm(fklngth ~ age, data = esturgeon.male)

Rien n’apparait à l’écran, c’est normal ne vous inquiétez pas, tout a été sauvegardé en mémoire (nouvel objet visible dans l’onglet environnement) . Pour voir les résultats, tapez:

summary(RegModele.1)

Call:
lm(formula = fklngth ~ age, data = esturgeon.male)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.4936 -2.2263  0.1849  1.7526 10.8234 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 28.50359    1.16873   24.39   <2e-16 ***
age          0.70724    0.05888   12.01   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.307 on 73 degrees of freedom
  (5 observations deleted due to missingness)
Multiple R-squared:  0.664, Adjusted R-squared:  0.6594 
F-statistic: 144.3 on 1 and 73 DF,  p-value: < 2.2e-16

la sortie R donne:

  1. Call: Un petit rappel du modèle qui a été ajusté et des données utilisées.
  2. Residuals: Un sommaire statistique des résidus autour du modèle estimé.
  3. Coefficients: Valeurs estimées des paramètres du modèle, erreurs-types, statistiques t et probabilités associées.
  4. Residual standard error: Racine carrée de la variance résiduelle.
  5. Multiple R-squared: Coefficient de détermination. Il correspond à la proportion de la variabilité de la variable dépendante qui peut être expliquée par la régression.
  6. Adjusted R-squared: Le R-carré ajusté tient compte du nombre de paramètres du modèle. Si vous voulez comparer différents modèles qui n’ont pas le même nombre de paramètres, c’est ce qu’il faut utiliser.
  7. F-statistic: C’est le test de signification omnibus du modèle. Dans le cas de la régression simple, il est équivalent au test sur la pente de la régression.

La régression estimée est donc:

\[ Fklngth = 28.50359 + 0.70724 * age\]

Étant donné la valeur significative du test de F (ainsi que pour le test de t pour la pente de la droite), on rejette l’hypothèse nulle qu’il n’y a pas de relation entre la taille et l’âge.

9.6.1 Vérifier les conditions d’application de la régression

La régression simple de type I a quatre conditions préalables :

  1. il n’y a pas d’erreur de mesure sur la variable indépendante (X)
  2. la relation entre Y et X est linéaire
  3. les résidus sont normalement distribués
  4. la variance des résidus est constante pour toutes les valeurs de la variable indépendante (homoscedasticité)

Procédons maintenant à l’examen post-mortem. La première condition est rarement remplie avec des données biologiques ; il y presque toujours de l’erreur sur X et sur Y. Cela veut dire qu’en général les pentes estimées sont biaisées, mais que les valeurs prédites ne le sont pas. Toutefois, si l’erreur de mesure sur X est petite par rapport à l’étendue des valeurs de X, le résultat de l’analyse n’est pas dramatiquement influencé. Par contre, si l’erreur de mesure est relativement grande (toujours par rapport à l’étendue des valeurs de X), la droite de régression obtenue par la régression de modèle I est un piètre estimé de la relation fonctionnelle entre X et Y. Dans ce cas, il est préférable de passer à la régression de modèle II, malheureusement au-delà du contenu de ce cours. Les autres conditions préalables à l’analyse de régression de modèle I peuvent cependant être vérifiées, ou du moins évaluées visuellement. La fonction plot() (appliqué directement sur un objet de type model) permet de visualiser des graphiques diagnostiques pour des modèles linéaires.

par(mfrow = c(2, 2), las = 1)
plot(RegModele.1)

La fonction par() est utilisée pour dire à R de tracer 2 rangées et 2 colonnes de graphiques par page (il y a quatre graphiques diagnostiques qui sont générés automatiquement pour les modèles linéaires), et l’argument las = indique à R d’effectuer une rotation des légendes des axes Y pour qu’elles soient perpendiculaires à l’axe (oui. Je sais. Rien de tout ça n’est évident.)

Vous obtiendrez:

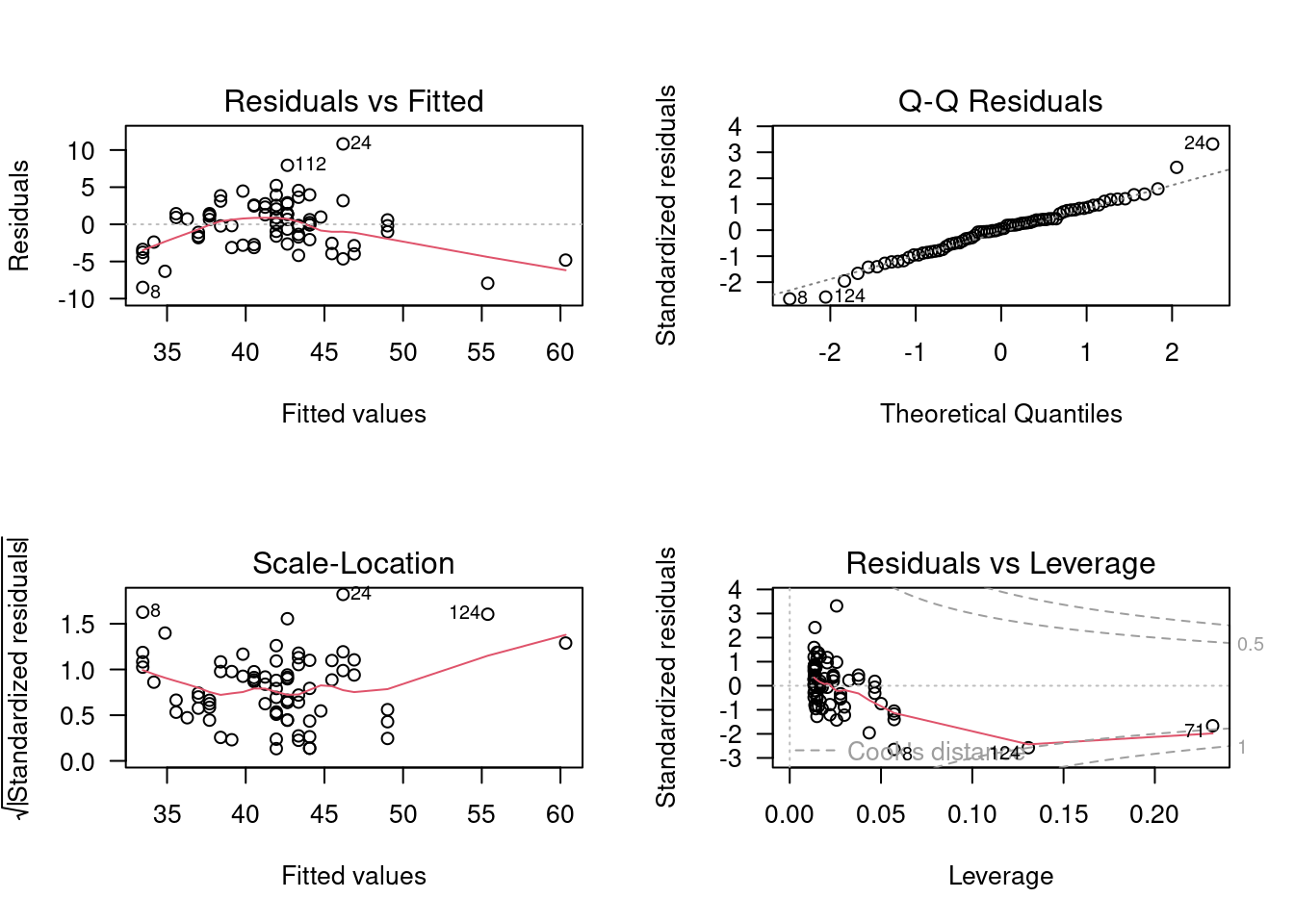
Figure 9.6: Graphiques diagnostiques du modèle.
  1. Le graphique en haut à gauche, permet d’évaluer la linéarité, la normalité, et l’homoscédasticité des résidus. Il illustre les déviations autour de la régression en fonction des valeurs prédites. Rappelez-vous que le graphique de fklngth vs age suggère que la relation entre la longueur et l’âge n’est pas linéaire. Les très jeunes et très vieux esturgeons sont sous la droite en général, alors que les esturgeons d’âge moyen sont retrouvés généralement au-dessus de la droite de régression. C’est exactement ce que le graphique des résidus en fonction des valeurs prédites illustre. La ligne en rouge est une trace “lowess” au travers de ce nuage de points. Si la relation était linéaire, la trace “lowess” serait presque plate et près de 0. La dispersion des résidus permet d’évaluer visuellement leur normalité et hétéroscédasticité; mais ce graphique n’est pas optimal pour évaluer ces propriétés. Les deux graphiques suivants sont mieux pour cela.
  2. Le graphique en haut à droite permet d’évaluer la normalité des résidus. C’est un graphique QQ des résidus (QQ plot). Des résidus distribués normalement tomberaient exactement sur la diagonale. Ici, on voit que c’est presque le cas, sauf dans les queues de la distribution.
  3. Le graphique en bas à gauche, intitulé Scale-Location, permet d’évaluer l’homoscédasticité. On y retrouve sur l’ordonnée (l’axe des y) la racine carrée de la valeur absolue des résidus standardisés (résidus divisés par l’écart-type des résidus) en fonction des valeurs prédites. Le graphique aide à déterminer si la variation des résidus est constante ou non. Si les résidus sont homoscédastiques, la valeur moyenne sur l’axe des y ne va pas changer en fonction de la valeur prédite. Ici, il y a une certaine tendance, mais pas une tendance monotone puisqu’il y a d’abord une baisse puis une hausse..; bref, rien qui soit une forte évidence contre la supposition d’homoscédasticité.
  4. Le graphique en bas à droite, montre les résidus en fonction du “leverage” et permet de détecter certaines valeurs extrêmes qui ont une grande influence sur la régression. Le leverage d’un point mesure sa distance des autres points, mais seulement en ce qui concerne les variables indépendantes. Dans le cas d’une régression simple, cela revient à la distance entre le point sur l’axe des x et la moyenne de tous les points sur cet axe. Vous devriez porter une attention particulière aux observations qui ont un leverage plus grand que \(2(k+1)/n\), où k est le nombre de variables indépendantes (ici, 1) et n est le nombre d’observations. Dans cet exemple, il y a 75 observations et une variable indépendante et donc les points ayant un leverage plus grand que \(4 / 75 = 0.053\) devrait être considérés avec attention. Le graphique indique également comment la régression changerait si on enlevait un point. Ce changement est mesuré par la distance de Cook, illustrée par les bandes en rouge sur le graphique. Un point ayant une distance de Cook supérieure à 1 a une grande influence.
Avertissement

Notez que R identifie automatiquement les cas les plus extrêmes sur chacun de ces 4 graphiques. Le fait qu’un point soit identifié ne signifie pas nécessairement que c’est une valeur réellement extrême, ou que vous devez vous en préoccuper. Dans tous les ensembles de données il y aura toujours un résidu plus grand que les autres…

Il est possible d’obtenir des graphiques d’évaluations des conditions d’applications, qui sont plus simple à interpréter et plus joli (avec des couleurs). On peut utiliser la fonction check_model() du paquet performance 📦.

check_model(RegModele.1)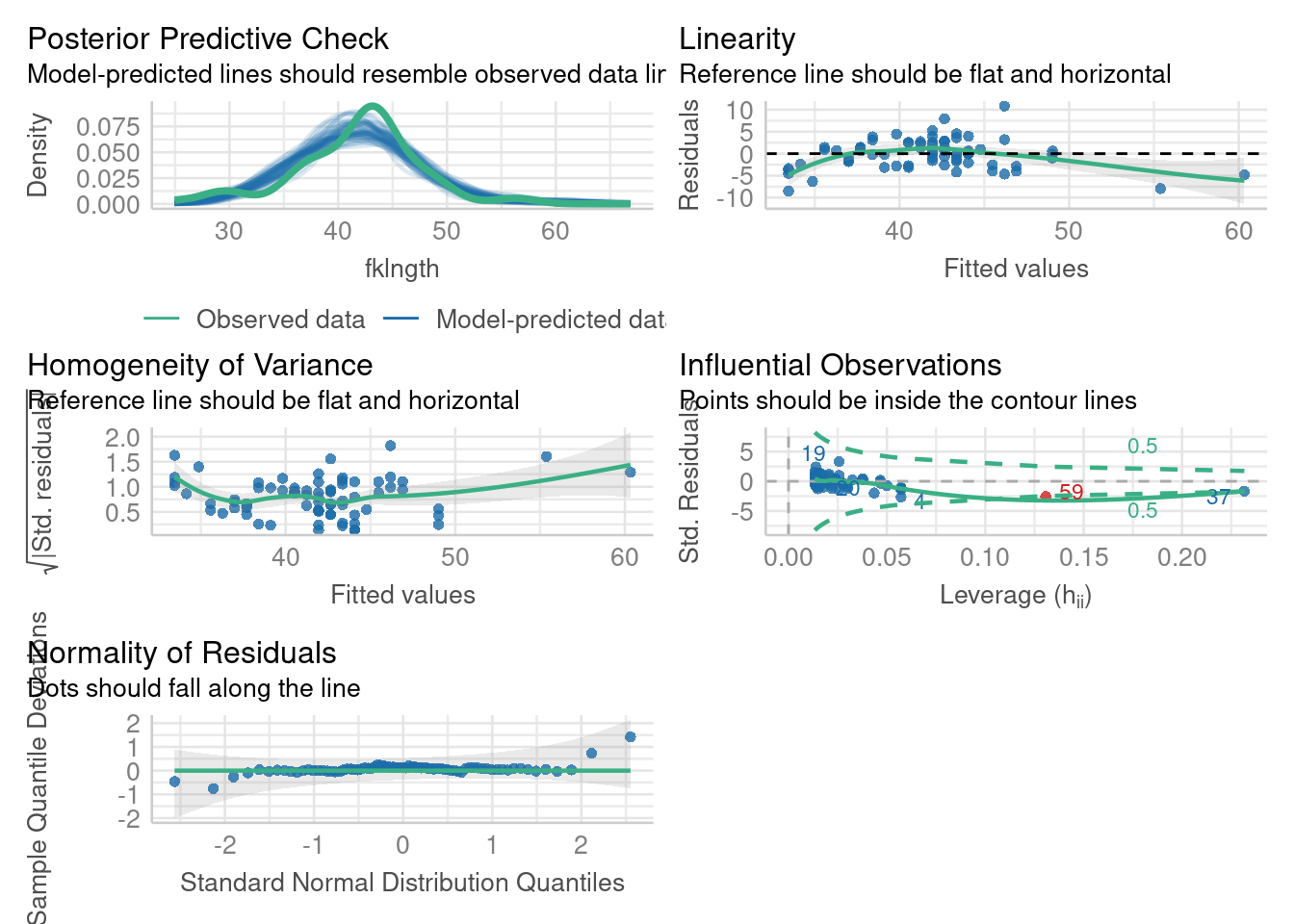
Figure 9.7: Graphiques diagnostiques du modèle avec la fonction check_model().

Finalement, quel est le verdict concernant la régression linéaire entre fklngth et age ? Elle viole la condition de linéarité, possiblement celle de normalité, remplit la condition d’homoscédasticité, et ne semble pas être influencée outre mesure par des valeurs bizarres ou extrêmes.

9.6.2 Tests formels des conditions d’application pour la régression

Personnellement, je n’utilise jamais les tests formels des conditions d’application de la régression et me contente des graphiques des résidus pour guider mes décisions. C’est ce que la plupart des praticiens font. Cependant, lors de mes premières analyses, je n’étais pas toujours certain de bien interpréter les graphiques et j’aurais aimé un indice plus formel ou un test permettant de détecter les violations des conditions d’application de la régression.

Le package lmtest 📦 (disponible sur CRAN), permet de faire plusieurs tests de linéarité et d’homoscédasticité. Et on peut tester la normalité avec le test Shapiro-Wilk vu précédemment.

Charger le package lmtest de CRAN (et installer le si besoin).

library(lmtest)
Exercice

Exécutez les commandes suivantes

bptest(RegModele.1)

    studentized Breusch-Pagan test

data:  RegModele.1
BP = 1.1765, df = 1, p-value = 0.2781

Le test Breusch-Pagan examine si la variabilité des résidus est constantes lorsque les valeurs prédites changent. Une faible valeur de p suggère de l’hétéroscédasticité. Ici, la valeur p est élevée et suggère que la condition d’application d’homoscédasticité est remplie avec ces données.

dwtest(RegModele.1)

    Durbin-Watson test

data:  RegModele.1
DW = 2.242, p-value = 0.8489
alternative hypothesis: true autocorrelation is greater than 0

Le test Durbin-Watson permet de détecter l’autocorrélation sérielle des résidus. En l’absence d’autocorrélation (i.e. d’indépendance des résidus) la valeur attendue de la statistique D est 2. Ce test permet d’éprouver l’hypothèse d’indépendance des résidus, mais ne permet de détecter qu’un type particulier de dépendance. Ici, le test ne permet pas de rejeter l’hypothèse d’indépendance.

resettest(RegModele.1)

    RESET test

data:  RegModele.1
RESET = 14.544, df1 = 2, df2 = 71, p-value = 5.082e-06

Le test RESET permet d’éprouver la linéarité. Si la relation est linéaire, alors la statistique RESET sera d’environ 1. Ici, la statistique est beaucoup plus élevée (14.54) et hautement significative. Le test confirme la tendance que nous avons détectée visuellement plus haut: la relation n’est pas linéaire.

shapiro.test(residuals(RegModele.1))

    Shapiro-Wilk normality test

data:  residuals(RegModele.1)
W = 0.98037, p-value = 0.2961

Le test de normalité Shapiro-Wilk sur les résidus confirme que la déviation par rapport à une distribution normale des résidus n’est pas grande.

9.7 Transformation des données en régression

La relation entre fklngth et age n’étant pas linéaire, on devrait donc essayer de transformer les données pour tenter de les linéariser :

  • Voyons ce qu’une transformation log donne:
par(mfrow = c(1, 1), las = 1)
ggplot(
  data = esturgeon.male,
  aes(x = log10(age), y = log10(fklngth))
) +
  geom_smooth(color = "red") +
  geom_smooth(method = "lm", se = FALSE, color = "green") +
  geom_point()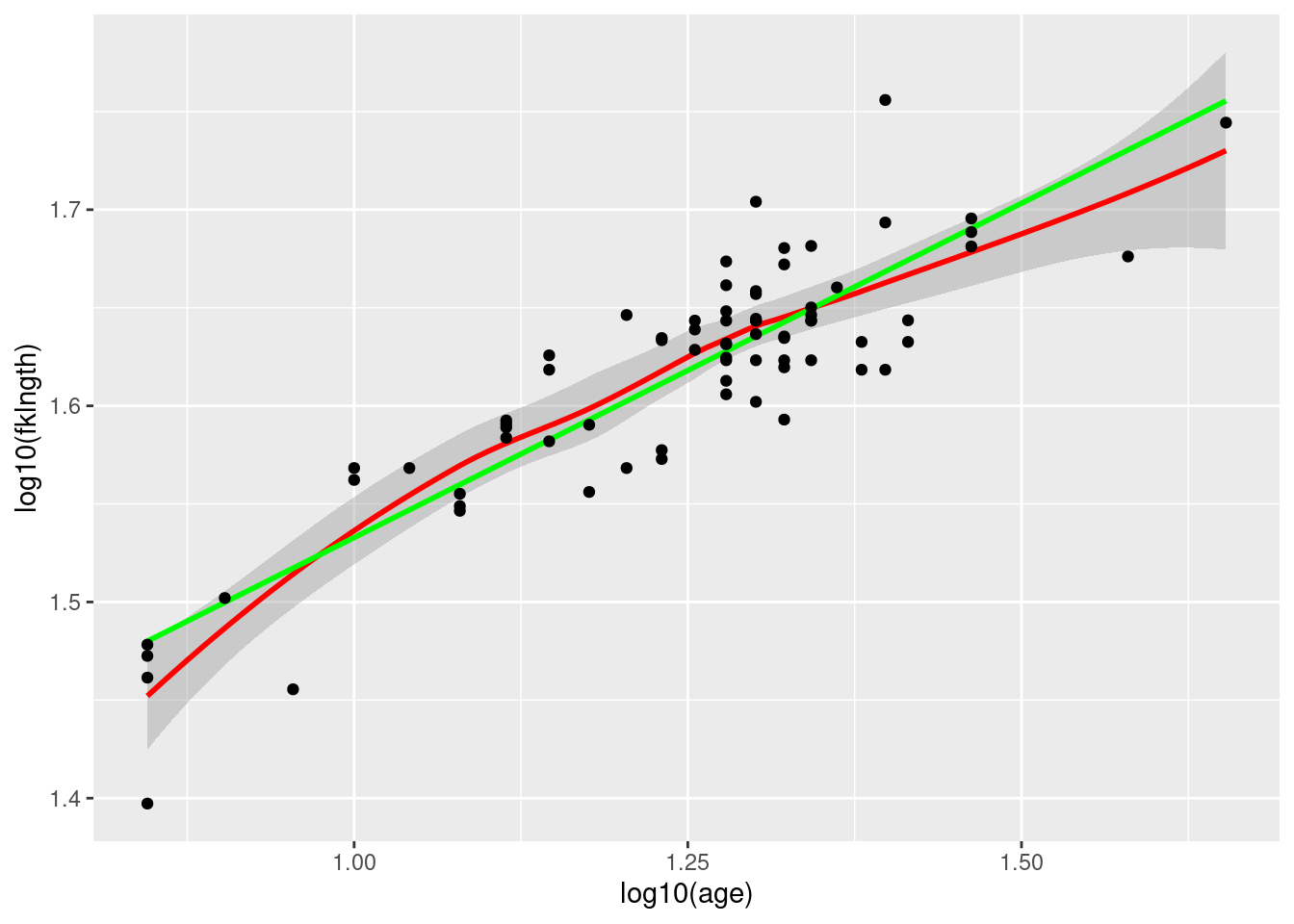
Figure 9.8: Graphique du log de la longueur en fonction du log de l’âge des esturgeons males

Ajustons maintenant une régression simple sur ces données transformées.

RegModele.2 <- lm(log10(fklngth) ~ log10(age), data = esturgeon.male)
summary(RegModele.2)

Call:
lm(formula = log10(fklngth) ~ log10(age), data = esturgeon.male)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.082794 -0.016837 -0.000719  0.021102  0.087446 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.19199    0.02723   43.77   <2e-16 ***
log10(age)   0.34086    0.02168   15.72   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.03015 on 73 degrees of freedom
  (5 observations deleted due to missingness)
Multiple R-squared:  0.772, Adjusted R-squared:  0.7688 
F-statistic: 247.1 on 1 and 73 DF,  p-value: < 2.2e-16

Examinons maintenant les graphiques diagnostiques:

par(mfrow = c(2, 2), las = 1)
plot(RegModele.2)
Figure 9.9: Graphiques diagnostiques du modèle avec les données log-transformées.

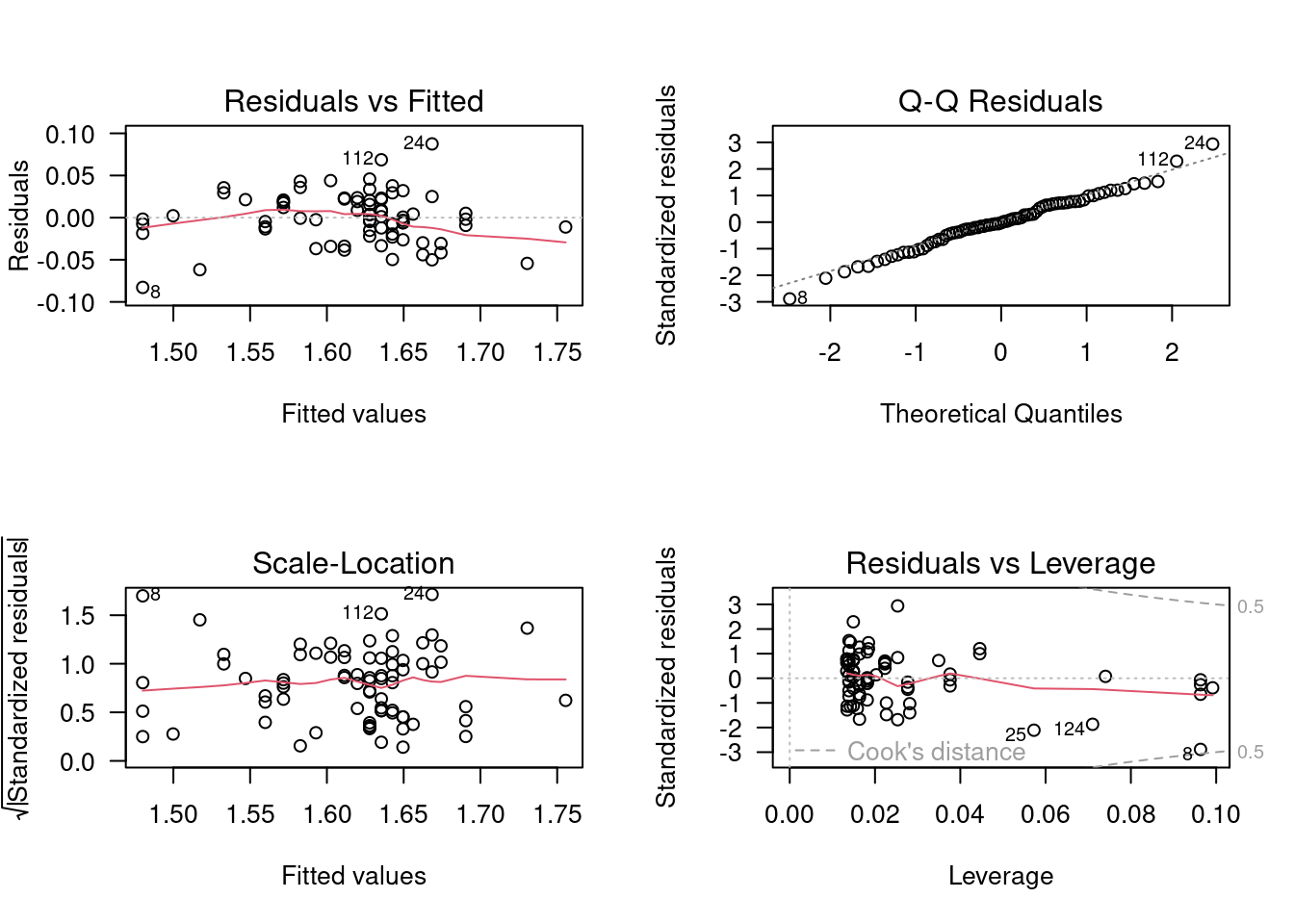
Il y a une certaine amélioration, mais ce n’est pas encore parfait (la perfection n’est pas de ce monde….). Le graphique des résidus en fonction des valeurs prédites suggère encore une certaine non linéarité. Sur le graphique Q-Q les points se retrouvent plus près de la droite diagonale qu’avant, indiquant que les résidus sont encore plus près de la normalité après la transformation log-log. Il n’y a pas d’indice d’hétéroscédasticité. Finalement, même si il reste quelques points avec plus d’influence (leverage) que les autres, aucun n’a une distance de Cook au-delà de 0.5. En résumé, la transformation log a amélioré les choses: la relation est plus linéaire, les résidus sont plus normaux, et il y a moins de points avec une influence relativement élevée. Est-ce que les tests formels supportent cette évaluation ?

bptest(RegModele.2)

    studentized Breusch-Pagan test

data:  RegModele.2
BP = 0.14282, df = 1, p-value = 0.7055
dwtest(RegModele.2)

    Durbin-Watson test

data:  RegModele.2
DW = 2.1777, p-value = 0.6134
alternative hypothesis: true autocorrelation is greater than 0
resettest(RegModele.2)

    RESET test

data:  RegModele.2
RESET = 4.4413, df1 = 2, df2 = 71, p-value = 0.01523
shapiro.test(residuals(RegModele.2))

    Shapiro-Wilk normality test

data:  residuals(RegModele.2)
W = 0.98998, p-value = 0.8246

Oui, les conclusions sont les mêmes: les résidus sont encore homoscédastiques (test Breusch-Pagan), ne sont pas autocorrélés (test Durbin-Watson), sont normaux (test Shapiro-Wilk), et sont plus linéaires (la valeur de P du test RESET est maintenant 0.015, au lieu de 0.000005). Donc la linéarité a augmenté, mais cette condition d’application semble encore légèrement violée.

9.8 Traitement des valeurs extrêmes

Dans cet exemple, il n’y a pas de valeur vraiment extrême. Oui, je sais, R a quand même identifié les observations 8, 24, et 112 dans le dernier graphique diagnostique. Mais ces valeurs sont encore dans la fourchette de valeurs que je juge “acceptables”. Mais comment déterminer objectivement ce qui est acceptable ? À quel moment juge t’on qu’une valeur extrême est vraiment trop invraisemblable pour ne pas l’exclure ? Il n’y a malheureusement pas de règle absolue là-dessus. Les opinions varient, mais je penche vers le conservatisme sur cette question.

Ma position est que, à moins que la valeur soit biologiquement impossible ou clairement une erreur d’entrée de données, je n’élimine pas les valeurs extrêmes et j’utilise toutes mes données dans leur analyse. Pourquoi?

Parce que je veux que mes données reflètent bien la variabilité naturelle ou réelle. C’est d’ailleurs parfois cette variabilité qui est intéressante.

L’approche conservatrice qui consiste à conserver toutes les valeurs extrêmes possibles est possiblement la plus honnête, mais elle peut causer certains problèmes. Ces valeurs extrêmes sont souvent la cause des violations des conditions d’application des tests statistiques. La solution suggérée à ce dilemme est de faire l’analyse avec et sans les valeurs extrêmes et de comparer les conclusions. Dans bien des cas, les conclusions seront qualitativement les mêmes et les tailles d’effet ne seront pas très différentes. Toutefois, dans certains cas, la présence des valeurs extrêmes change complètement les conclusions. Dans ces cas, il faut simplement accepter que les conclusions dépendent entièrement de la présence des valeurs extrêmes et sont donc peu concluantes.

Suivant cette approche comparative, refaisons donc l’analyse après avoir enlevé les observations 8, 24, et 112.

RegModele.3 <- lm(log10(fklngth) ~ log10(age), data = esturgeon.male, subset = !(rownames(esturgeon.male) %in% c("8", "24", "112"))) # On enlève les observations 8, 24 et 112 du jeu de données
summary(RegModele.3)

Call:
lm(formula = log10(fklngth) ~ log10(age), data = esturgeon.male, 
    subset = !(rownames(esturgeon.male) %in% c("8", "24", "112")))

Residuals:
      Min        1Q    Median        3Q       Max 
-0.069163 -0.017390  0.000986  0.018590  0.047647 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.22676    0.02431   50.46   <2e-16 ***
log10(age)   0.31219    0.01932   16.16   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.02554 on 70 degrees of freedom
  (5 observations deleted due to missingness)
Multiple R-squared:  0.7885,    Adjusted R-squared:  0.7855 
F-statistic:   261 on 1 and 70 DF,  p-value: < 2.2e-16

L’ordonnée à l’origine (Intercept), la pente, et le R carré sont presque les mêmes, et la valeur de p est encore astronomiquement petite. Enlever les valeurs extrêmes a peu d’effet dans ce cas.

Les graphiques diagnostiques des résidus et les tests formels des conditions d’application sur ce sous-ensemble de données donnent :

par(mfrow = c(2, 2))
plot(RegModele.3)
bptest(RegModele.3)

    studentized Breusch-Pagan test

data:  RegModele.3
BP = 0.3001, df = 1, p-value = 0.5838
dwtest(RegModele.3)

    Durbin-Watson test

data:  RegModele.3
DW = 2.0171, p-value = 0.5074
alternative hypothesis: true autocorrelation is greater than 0
resettest(RegModele.3)

    RESET test

data:  RegModele.3
RESET = 3.407, df1 = 2, df2 = 68, p-value = 0.0389
shapiro.test(residuals(RegModele.3))

    Shapiro-Wilk normality test

data:  residuals(RegModele.3)
W = 0.98318, p-value = 0.4502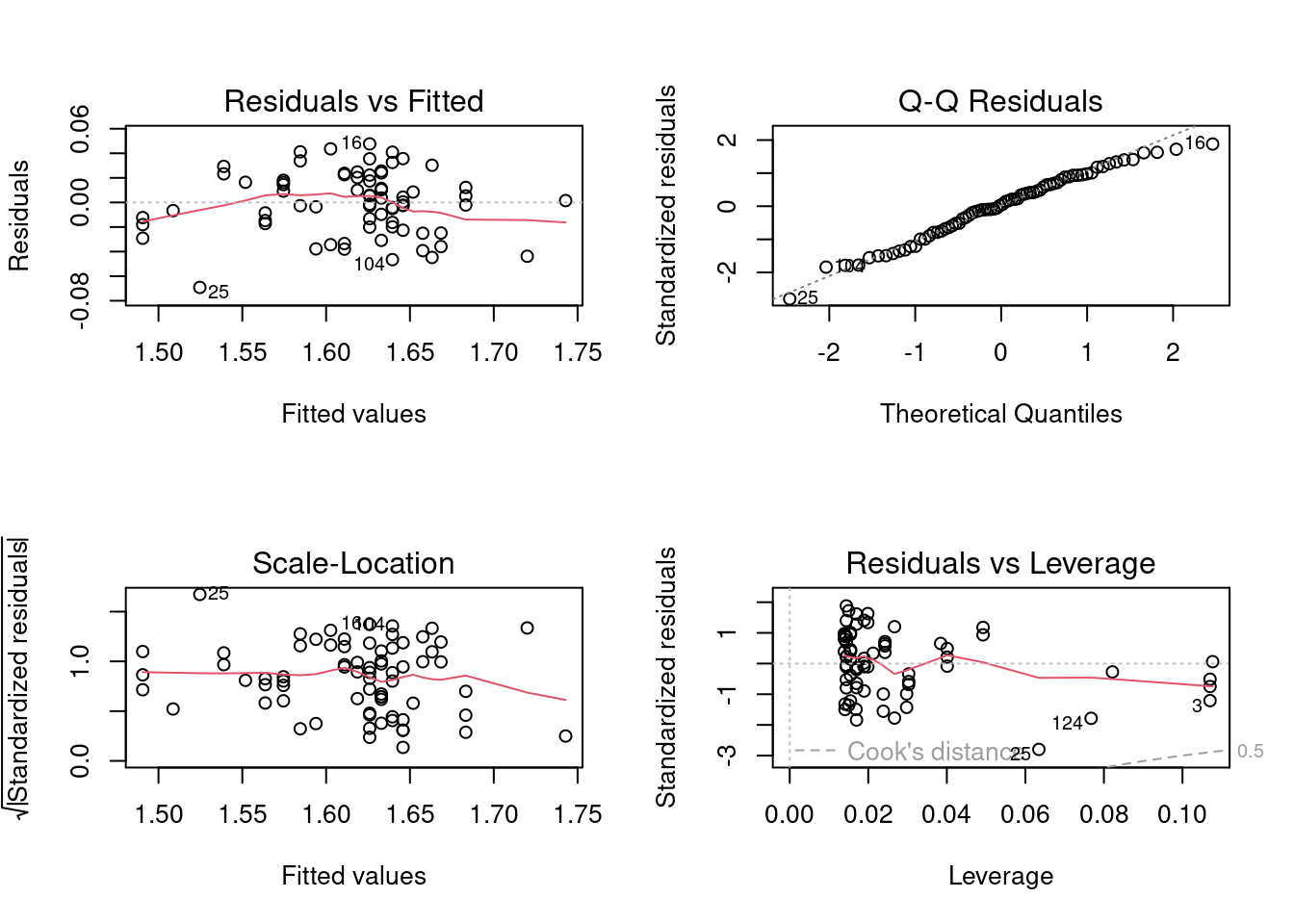
Figure 9.10: Graphiques diagnostiques du modèle RegModele.3 excluant les données aberrantes.

Il n’y a pas vraiment de différence ici non plus avec l’analyse des données en entier. Bref, tout pointe vers la conclusion que les valeurs les plus extrêmes de cet ensemble de donnée n’influencent pas indûment les résultats statistiques.

9.9 Quantifier la taille d’effet et analyse de puissance en régression

L’interprétation biologique des résultats n’est pas la même chose que l’interprétation statistique. Dans l’analyse qui précède, on conclue statistiquement que la taille augmente avec l’âge (puisque la pente est positive et et \(p<0.05\)). Mais cette augmentation “statistique” de la taille avec l’âge ne donne pas d’informations sur la différence de taille entre les jeunes et vieux individus. La pente et un graphique sont plus informatifs à ce sujet que la valeur p. La pente (dans l’espace log-log) est de 0.34. Cela veut dire que pour chaque unité d’accroissement de X (log10(age)), il y a une augmentation de 0.34 unités de log10(fklngth). En d’autres mots, quand l’âge est multiplié par 10, la longueur est multipliée environ par 2 (100.34 = 2.19). Donc la longueur des esturgeons augmente plus lentement que leur âge. La valeur de la pente (0.34) est un estimé de la taille de l’effet de l’âge sur la longueur.

Il est aussi important d’estimer l’intervalle de confiance sur la pente pour pouvoir estimer si l’intervalle n’inclus ou non que des valeurs biologiquement importantes. Cela peut être fait simplement avec la fonction confint().

confint(RegModele.2)
                2.5 %   97.5 %
(Intercept) 1.1377151 1.246270
log10(age)  0.2976433 0.384068

L’intervalle de confiance à 95% de la pente est 0.29-0.38. L,intervalle de confiance est assez étroit et éloigné de zéro.

9.9.1 Puissance de détecter une pente donnée

Pour les calculs de puissance avec G*Power vous devrez cependant utiliser une autre métrique de la taille de l’effet, calculée à partir de la pente, de son erreur-type, et de la taille de l’échantillon (ce qui facilite les calculs pour G*Power, mais malheureusement pas pour vous) La métrique (d) est calculée comme: \[ d = \frac{b}{s_b\sqrt{n-k-1}} \] où \(b\) est l’estimé de la pente, \(s_b\) est l’erreur type de la pente, \(n\) est le nombre d’observations, et \(k\) est le nombre de variables indépendantes (1 pour la régression linéaire simple).

Vous pouvez calculer approximativement la puissance avec G*Power pour une valeur de pente que vous jugez assez grande pour mériter d’être détectée. Choisissez Tests: Means: One group: difference from constant, là, vous devrez remplacer la valeur de \(b\) dans l’équation pour la taille d’effet (d) par la pente que vous voudriez détecter, mais utiliser l’erreur type calculée à partir de vos données.

Par exemple, supposons que les ichthyologues considèrent qu’une pente de 0.1 pour la relation entre log10(fklngth) et log10(age) est signifiante biologiquement, et qu’ils désirent estimer la puissance de détecter une telle pente à partir d’un échantillon de 20 esturgeons. Les résultats de la régression log-log nous fournissent ce dont on a besoin:

summary(RegModele.2)

Call:
lm(formula = log10(fklngth) ~ log10(age), data = esturgeon.male)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.082794 -0.016837 -0.000719  0.021102  0.087446 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.19199    0.02723   43.77   <2e-16 ***
log10(age)   0.34086    0.02168   15.72   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.03015 on 73 degrees of freedom
  (5 observations deleted due to missingness)
Multiple R-squared:  0.772, Adjusted R-squared:  0.7688 
F-statistic: 247.1 on 1 and 73 DF,  p-value: < 2.2e-16

L’erreur-type de la pente est 0.02168. Il y avait 75 poissons (n=75) dans l’échantillon de départ. On peut donc calculer la métrique de taille d’effet pour G*Power \[ d = \frac{b}{s_b\sqrt{n-k-1}} = \frac{0.1}{0.02168\sqrt{74-1-1}}=0.54\]

Armés de cette taille d’effet (une pente présumée de 0.1 et une variabilité autour de la régression similaire à la régression de fklngth vs age), choisissez Tests: Means: One group: difference from constant, et entrez la valeur calculée de d, alpha, et l’effectif de l’échantillon pour calculer la puissance.

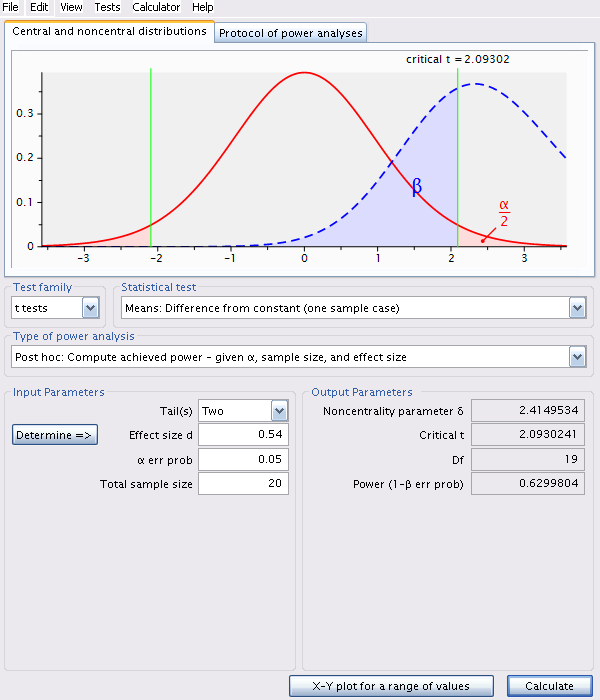
Figure 9.11: Analyse de puissance pour N = 20 et pente = 0.1

Dans R, il est possible de faire cette analyse avec le code suivant:

library(pwr)

# analyse de puissance
pwr.t.test(n = 20, d = 0.54, sig.level = 0.05, type = "one.sample")

     One-sample t test power calculation 

              n = 20
              d = 0.54
      sig.level = 0.05
          power = 0.6299804
    alternative = two.sided

La puissance de détecter une pente comme étant statistiquement significative (au niveau alpha), si la pente est 0.1, que la variabilité résiduelle autour de la régression est semblable à celle de notre échantillon (ce qui revient à une taille d’effet de 0.54, pour un échantillon de 20 esturgeons et alpha=0.05) est de 0.629. Seulement environ 2/3 des échantillons de cette taille détecteraient un effet significatif de l’âge sur fklngth.

9.9.2 Effectif requis pour atteindre une puissance désirée (test A-priori)

Pour estimer la taille d’échantillon (effectif) requis pour avoir une puissance de 99% de détecter un effet de l’âge si la pente est 0.1 (sur une échelle log-log), avec alpha=0.05, on utilise la même valeur de d (0.54):

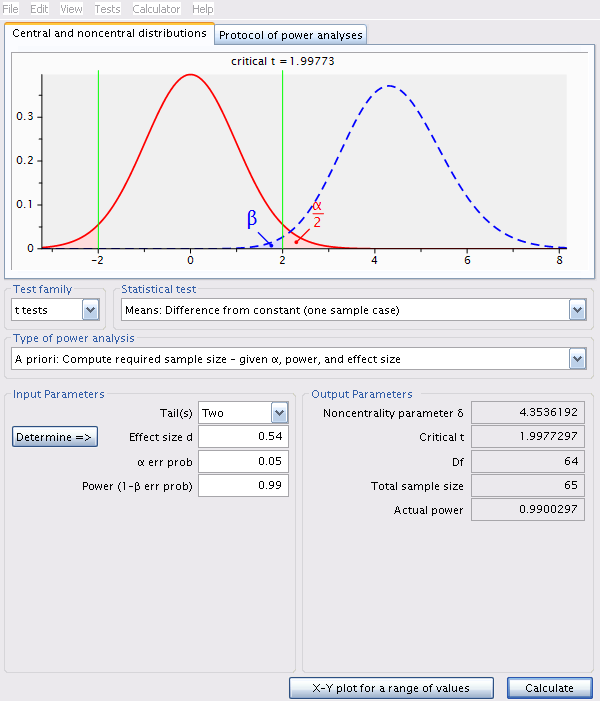
Figure 9.12: Analyse à priori pour déterminer la taille d’échantillon pour une puissance de 0.99

Dans R, il est possible de faire cette analyse avec le code suivant:

library(pwr)

# analyse de puissance
pwr.t.test(n = 65, d = 0.54, sig.level = 0.05, type = "one.sample")

     One-sample t test power calculation 

              n = 65
              d = 0.54
      sig.level = 0.05
          power = 0.9900297
    alternative = two.sided

En augmentant la taille de l’échantillon à 65, selon le même scénario que précédemment, la puissance augmente à 99%.

9.10 Bootstrap en régression simple avec R

Un test non paramétrique pour l’ordonnée à l’origine et la pente d’une régression simple peut être effectué par bootstrap.

# charger le paquet boot
library(boot)
# obtenir les poids de régression
bs <- function(formula, data, indices) {
  d <- data[indices, ] # Permets à boot de sélectionner les échantillons
  fit <- lm(formula, data = d)
  return(coef(fit))
}
# bootstrap avec 1000 réplications
results <- boot(
  data = esturgeon.male,
  statistic = bs,
  R = 1000, formula = log10(fklngth) ~ log10(age)
)
# Résultats
results

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = esturgeon.male, statistic = bs, R = 1000, formula = log10(fklngth) ~ 
    log10(age))


Bootstrap Statistics :
     original        bias    std. error
t1* 1.1919926  0.0010297189  0.03344522
t2* 0.3408557 -0.0006201354  0.02643693

Pour chaque paramètre du modèle (ici l’ordonnée à l’origine est appelée t1* et la pente de la régression t2*), R imprime :

  1. original la valeur estimée sur tout l’échantillon
  2. bias la différence entre la valeur moyenne des estimés par bootstrap et la valeur originale sur tout l’échantillon
  3. std. error l’erreur-type de l’estimé bootstrap
par(mfrow = c(2, 2))
plot(results, index = 1) # intercept
plot(results, index = 2) # log10(age)
Figure 9.13: Résultats du test de bootstrap non paramétrique
Figure 9.14: Résultats du test de bootstrap non paramétrique

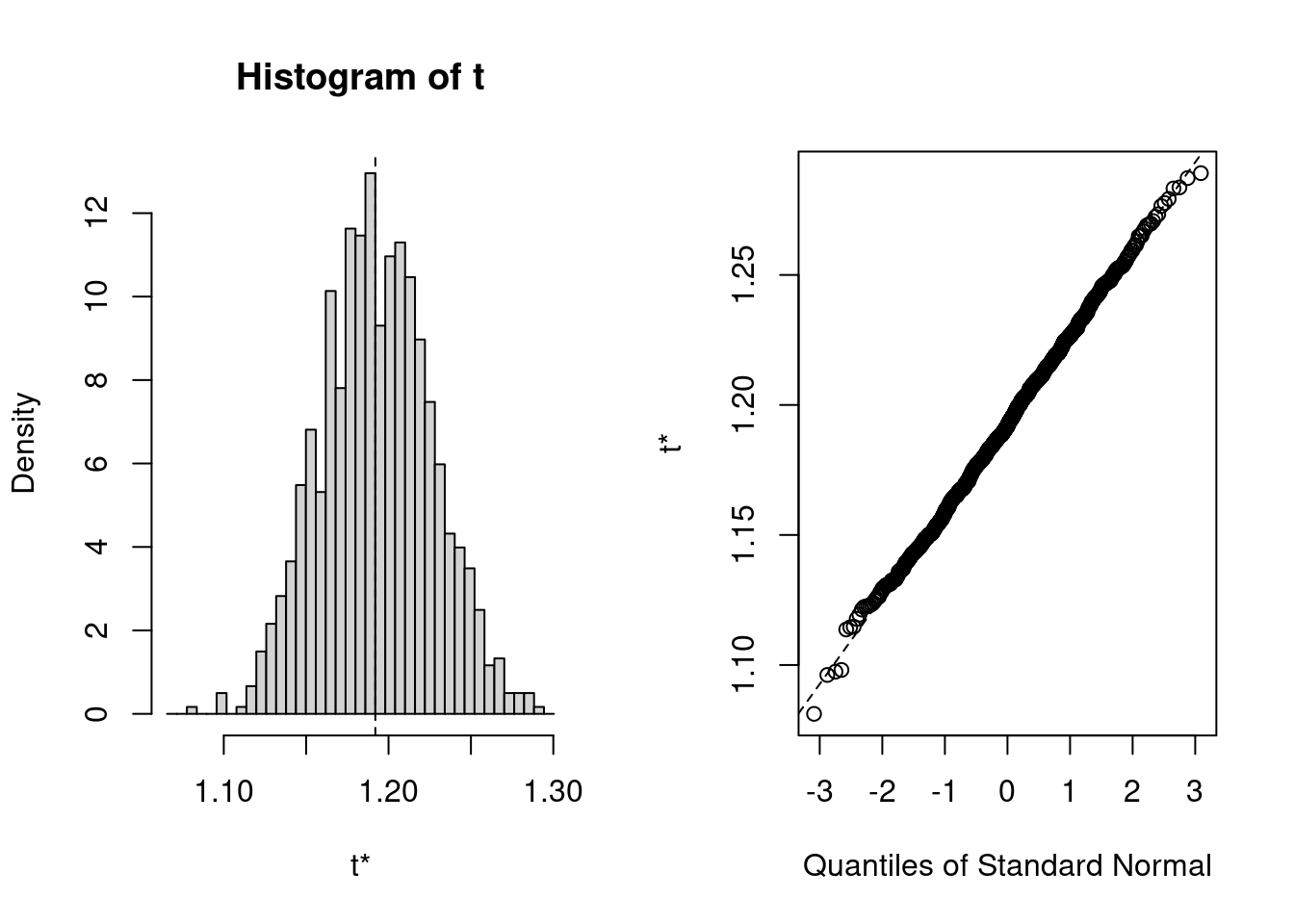
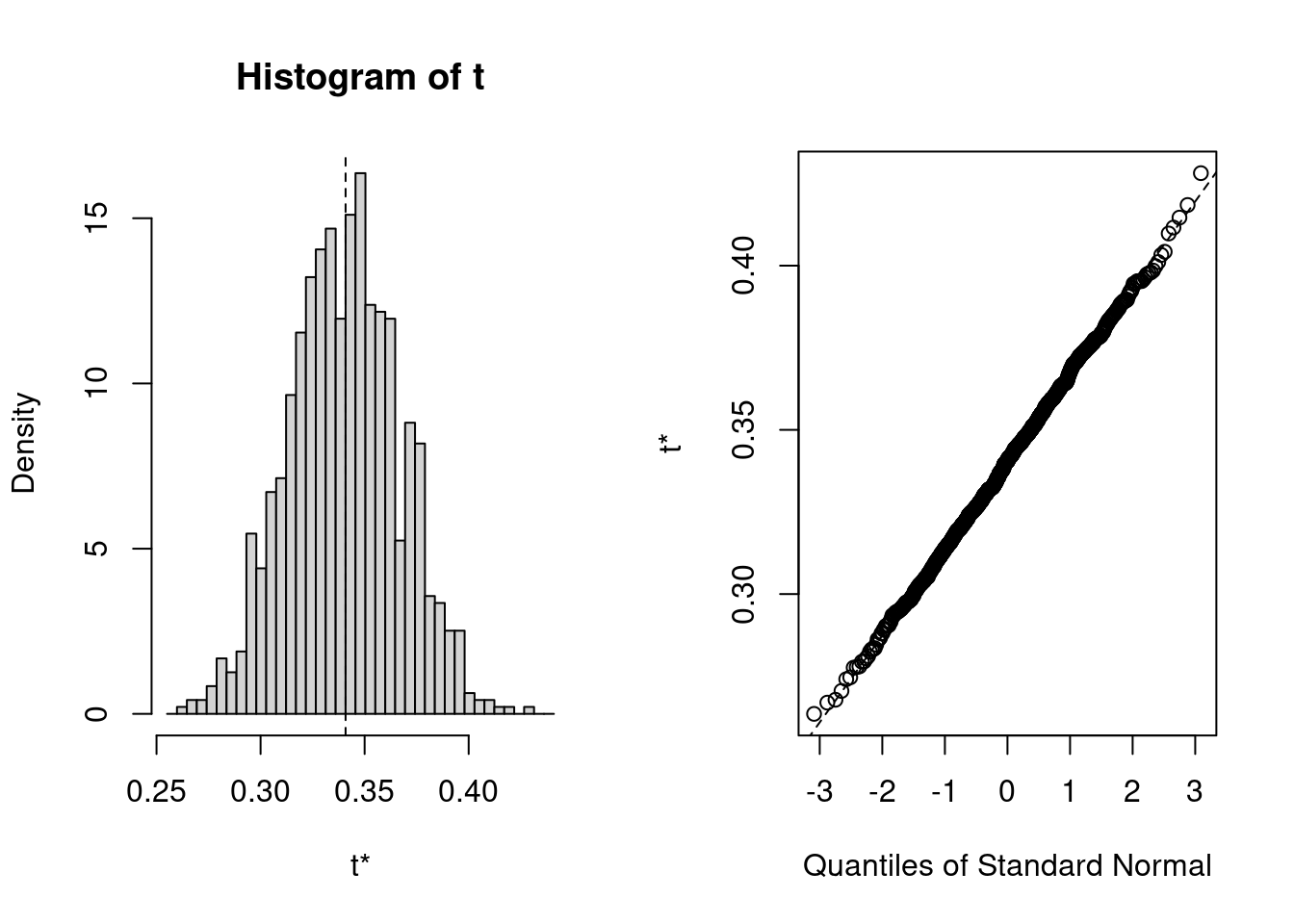
La distribution des estimés obtenus par bootstrap est assez normale dans cet exemple, avec de petites déviations dans les queue de la distribution (là où ça compte pour les intervalles de confiance…). On pourrait utiliser l’erreur-type des estimés bootstrap pour calculer un intervalle de confiance symétrique (moyenne +- t E.T.). Cependant, comme R peut facilement calculer des intervalles de confiance qui corrigent pour le biais (BCa: “Bias-Corrected Adjusted”) ou encore des intervalle empiriques à partir des distributions simulées (méthode Percentile) il peut être aussi simple de les calculer selon les 3 méthodes:

# interval de confiance pour l'ordonnée à l'origine
boot.ci(results, type = "all", index = 1)
Warning in boot.ci(results, type = "all", index = 1): bootstrap variances
needed for studentized intervals
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates

CALL : 
boot.ci(boot.out = results, type = "all", index = 1)

Intervals : 
Level      Normal              Basic         
95%   ( 1.125,  1.257 )   ( 1.126,  1.254 )  

Level     Percentile            BCa          
95%   ( 1.130,  1.258 )   ( 1.123,  1.253 )  
Calculations and Intervals on Original Scale
# intervalle de confiance pour la pente
boot.ci(results, type = "all", index = 2)
Warning in boot.ci(results, type = "all", index = 2): bootstrap variances
needed for studentized intervals
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates

CALL : 
boot.ci(boot.out = results, type = "all", index = 2)

Intervals : 
Level      Normal              Basic         
95%   ( 0.2897,  0.3933 )   ( 0.2896,  0.3923 )  

Level     Percentile            BCa          
95%   ( 0.2894,  0.3921 )   ( 0.2941,  0.3955 )  
Calculations and Intervals on Original Scale

Ici, les 4 types d’intervalles de confiance que R a calculé sont essentiellement semblables. Si les données avaient violé plus sévèrement les conditions d’application de la régression (normalité, homoscedasticité), alors les différentes méthodes (Normal, Basic, Percentile, et BCa) auraient divergé un peu plus. Lequel choisir alors? BCa est celui qui est préféré de la majorité des praticiens, présentement.