10  Comparaison de deux échantillons

Objectifs de ce chapitre:

10.1 Paquets R et données requises

Pour ce laboratoire, vous aurez besoin de :

  • Paquets R :
    • car 📦
    • lmtest 📦
    • boot 📦
    • lmPerm 📦
  • Jeux de données :
    • pwr 📦
    • “sturgeon.csv”
    • “skulldat_2020.csv”
library(car)
library(lmtest)
library(boot)
library(lmPerm)
library(ggplot2)
library(pwr)
esturgeon <- read.csv("data/sturgeon.csv")
crane <- read.csv("data/skulldat_2020.csv")

10.2 Examen visuel des données

Une des premières étapes dans toute analyse de données est l’examen visuel des données par des graphiques et statistiques sommaires pour avoir une idée des distributions sous-jacentes, des valeurs extrêmes et des tendances dans vos données. Cela commence souvent avec des graphiques de vos données (histogrammes, diagrammes de probabilité, boîte à moustache, etc.) qui vous permettent d’évaluer si vos données sont distribuées normalement (c-à-d, suivent une distribution normale), si elles sont corrélées les unes aux autres, ou s’il y a des valeurs suspectes dans le jeu de données.

Supposons que l’on veuille comparer la distribution des taille des esturgeons de The Pas et Cumberland House. La variable fklngth dans le jeu de données sturgeon.csv représente la longueur (en cm) de chaque poisson (mesurée de l’extrémité de la tête à la base de la fourche de la nageoire caudale). Pour commencer, examinons si cette variable est normalement distribuée. On ne va pas tester pour la normalité à ce stade-ci ; la présomption de normalité dans les analyses paramétriques s’applique aux résidus et non aux données brutes. Cependant, si les données brutes ne sont pas normales, vous avez, en général, une très bonne raison de soupçonner que les résidus ne suivront pas non plus une distribution normale.

Une excellente façon de comparer visuellement une distribution à la distribution normale est de superposer un histogramme des données observées à une courbe normale. Pour ce faire, il faut procéder en deux étapes :

  1. Indiquer à R que nous voulons créer un histogramme superposé à une courbe normale
  2. Spécifier qu’on veut que les graphiques soient faits pour les deux sites
  • En utilisant les données de sturgeon.csv, générez les histogrammes et les approximations des distributions normales ajustées aux données de fklngth à The Pas et Cumberland House.
# Utilisez le jeu de données "sturgeon" pour créer le graphique appelé "mongraph".
# Et définissez l'axe x, correspondant à "fklngth".
mongraph <- ggplot(data = esturgeon, 
                   aes(x = fklngth)) +
  xlab("Longueur à la fourche (cm)")

# Ajoutez des éléments au graphique (ggplot) "mongraph".
mongraph <- mongraph +
  geom_density() + # Ajoutez la densité des données, lissée.
  geom_rug() + # Ajoutez un "tapis" (barres en bas du graphe).
  geom_histogram(aes(y = ..density..),
                 color = "black", alpha = 0.3) +  # Ajoutez un histogramme noir, semi transparent.
  stat_function(fun = dnorm,
                args = list(mean = mean(esturgeon$fklngth),
                            sd = sd(esturgeon$fklngth)),
                color = "red") # Ajoutez une courbe normale en rouge, à partir de la moyenne et écart-type de "fklngth".

mongraph + facet_grid(. ~ location) # Affichez le graphe, par site.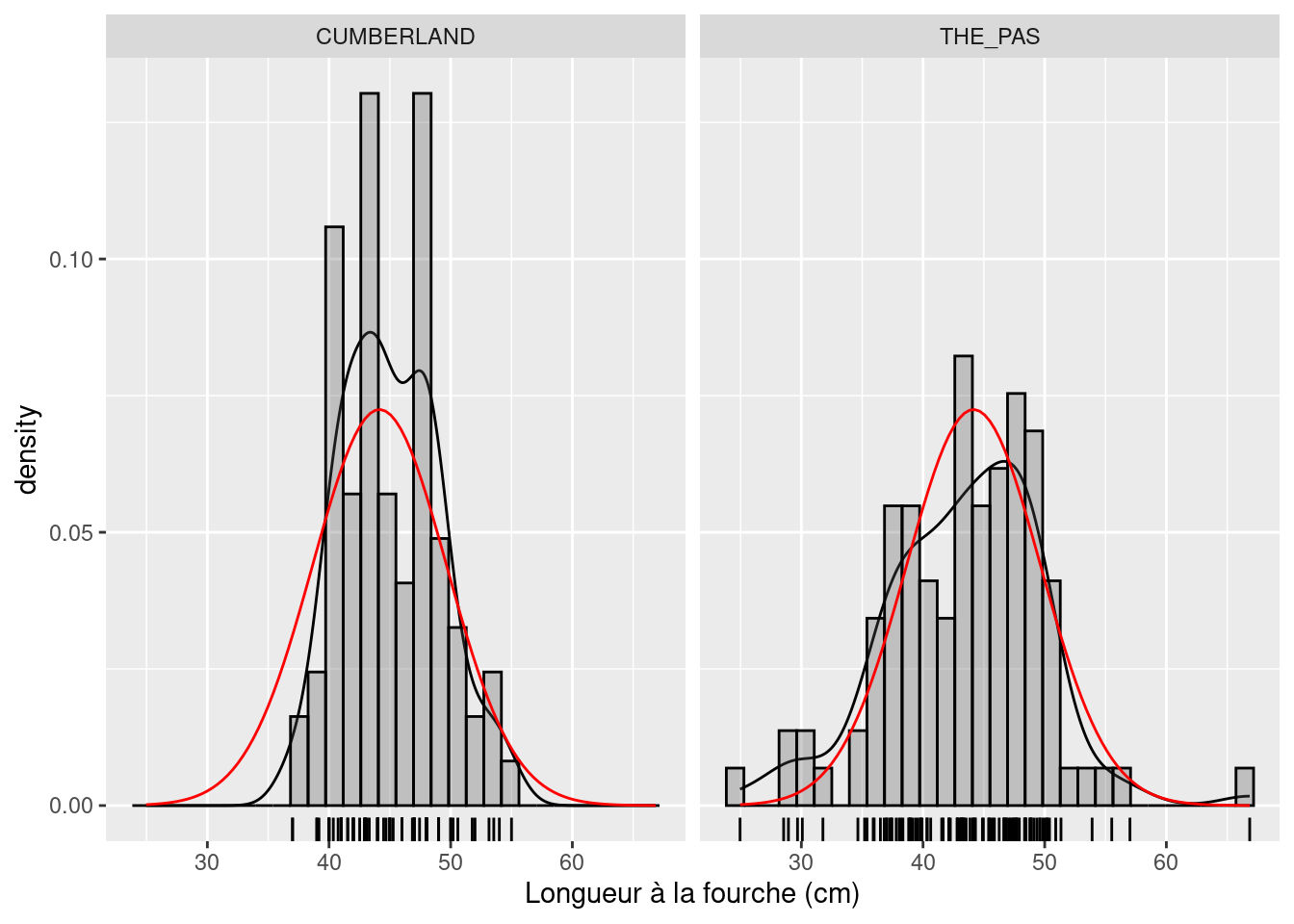
Figure 10.1: Distribution de la longueur des esturgeons par site.

Examinez ce graphique et essayez de déterminer si ces deux échantillons sont normalement distribués. À mon avis, cette variable est approximativement normalement distribuée dans les deux échantillons.

Puisque ce qui nous intéresse est de comparer la taille des poissons de deux sites différents, c’est probablement une bonne idée de créer un graphique qui compare les deux groupes de données. Une boîte à moustache (“Box plot”) convient très bien pour cette tâche.

  • Tracez un boxplot de fklngth groupé par location. Que concluez-vous quant à la différence entre les deux sites?
ggplot(data = esturgeon, aes(x = location, 
                            y = fklngth)) +
  geom_boxplot(notch = TRUE)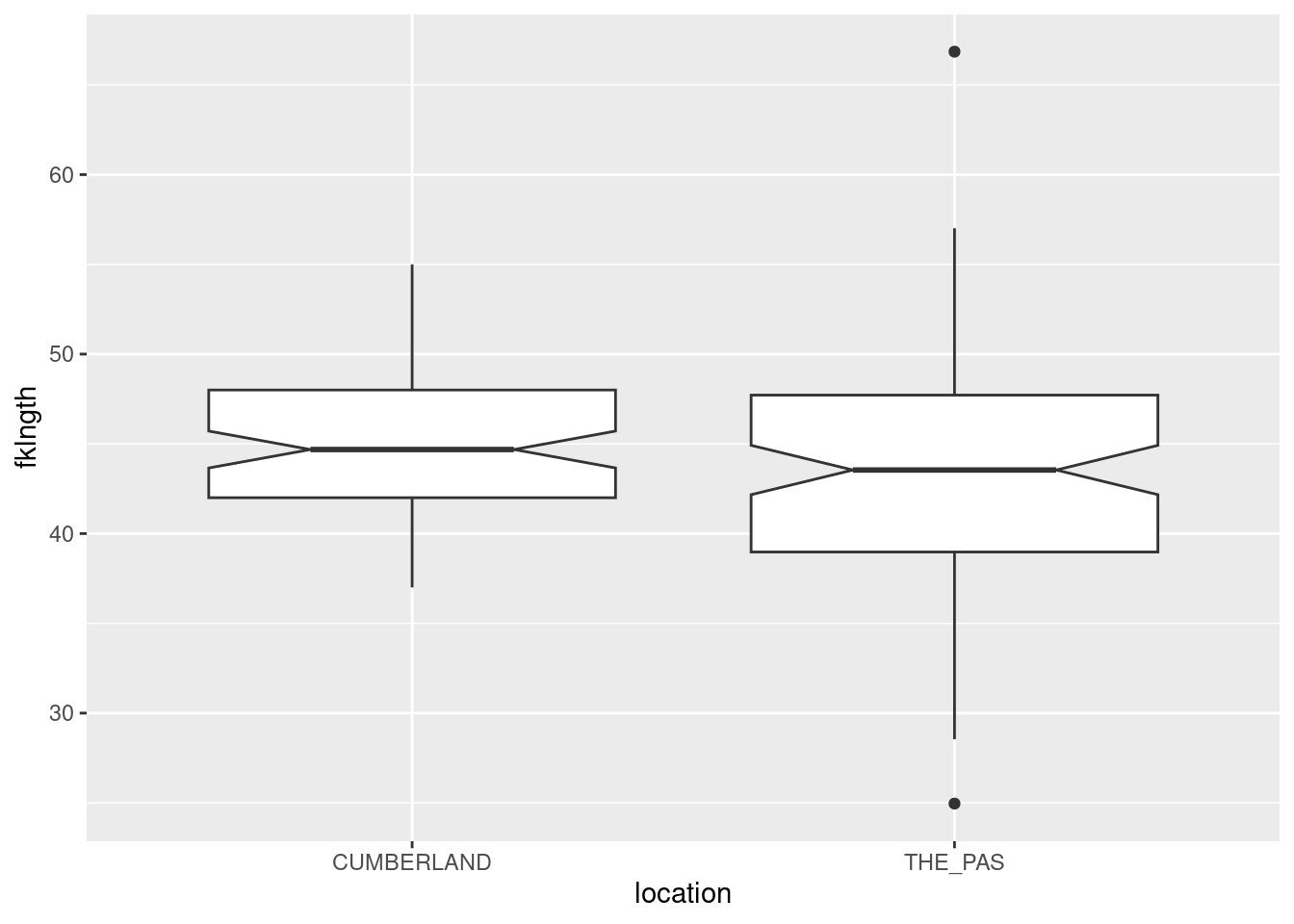
Figure 10.2: Boxplot de la longueur des esturgeons par site.

Il n’y a pas de grande différence de taille entre les deux sites, mais la taille des poissons à The Pas est plus variable, ayant une plus large étendue de taille et des valeurs extrêmes (définies par les valeurs qui sont > 1.5 * l’étendue interquartile) à chaque bout de la distribution.

10.3 Comparer les moyennes de deux échantillons indépendants

Éprouvez l’hypothèse nulle (H0) : La longueur à la fourche n’est pas différente entre The Pas et Cumberland House de 3 manières différentes :

  1. Test paramétriques supposant des variances égales
  2. Test paramétriques supposant des variances différentes
  3. Test non-paramétrique (pas de conditions d’applications sur la distribution et la variance)

Que concluez-vous?

# Test t supposant des variances égales.
t.test(fklngth ~ location,
       data = esturgeon,
       alternative = "two.sided",
       var.equal = TRUE)

    Two Sample t-test

data:  fklngth by location
t = 2.1359, df = 184, p-value = 0.03401
alternative hypothesis: true difference in means between group CUMBERLAND and group THE_PAS is not equal to 0
95 percent confidence interval:
 0.1308307 3.2982615
sample estimates:
mean in group CUMBERLAND    mean in group THE_PAS 
                45.08439                 43.36984 
# Test t supposant des variances différentes.
t.test(fklngth ~ location,
       data = esturgeon,
       alternative = "two.sided",
       var.equal = FALSE)

    Welch Two Sample t-test

data:  fklngth by location
t = 2.2201, df = 169.8, p-value = 0.02774
alternative hypothesis: true difference in means between group CUMBERLAND and group THE_PAS is not equal to 0
95 percent confidence interval:
 0.1900117 3.2390804
sample estimates:
mean in group CUMBERLAND    mean in group THE_PAS 
                45.08439                 43.36984 
# Test non paramétrique.
wilcox.test(fklngth ~ location,
            data = esturgeon,
            alternative = "two.sided")

    Wilcoxon rank sum test with continuity correction

data:  fklngth by location
W = 4973, p-value = 0.06296
alternative hypothesis: true location shift is not equal to 0

En se fiant au test de t, on rejette donc l’hypothèse nulle. Il y a une différence significative entre les deux moyennes des longueurs à la fourche selon le site.

Notez que si l’on se fie au test de Wilcoxon, on ne peut pas rejeter l’hypothèse nulle. Les deux tests mènent donc à des conclusions contradictoires. La différence significative obtenue par le test de t peut provenir en partie d’une violation des conditions d’application du test (normalité et homoscédasticité). D’un autre côté, l’absence de différence significative selon le test de Wilcoxon pourrait être due au fait que, pour un effectif donné, la puissance du test non paramétrique est inférieure à celle du test paramétrique correspondant. Compte tenu 1) des valeurs de p obtenues pour les deux tests, et 2) le fait que pour des grands échantillons (des effectifs de 84 et 101 sont considérés grands) le test de t est considéré robuste, il est raisonnable de rejeter l’hypothèse nulle.

Avant d’accepter les résultats du test de t et de rejeter l’hypothèse nulle qu’il n’y a pas de différences de taille entre les deux sites, il est important de déterminer si les données remplissent les conditions de normalité des résidus et d’égalité des variances. L’examen préliminaire suggérait que les données sont à peu près normales mais qu’il y avait peut-être des problèmes avec les variances (puisque l’étendue des données pour The Pas était beaucoup plus grande que celle pour Cumberland). On peut examiner ces conditions d’application plus en détail en examinant les résidus d’un modèle linéaire et en utilisant les graphiques diagnostiques:

m1 <- lm(fklngth ~ location, data = esturgeon)
par(mfrow = c(2, 2))
plot(m1)
Figure 10.3: Examen visuel des conditions d’application du modèle linéaire.

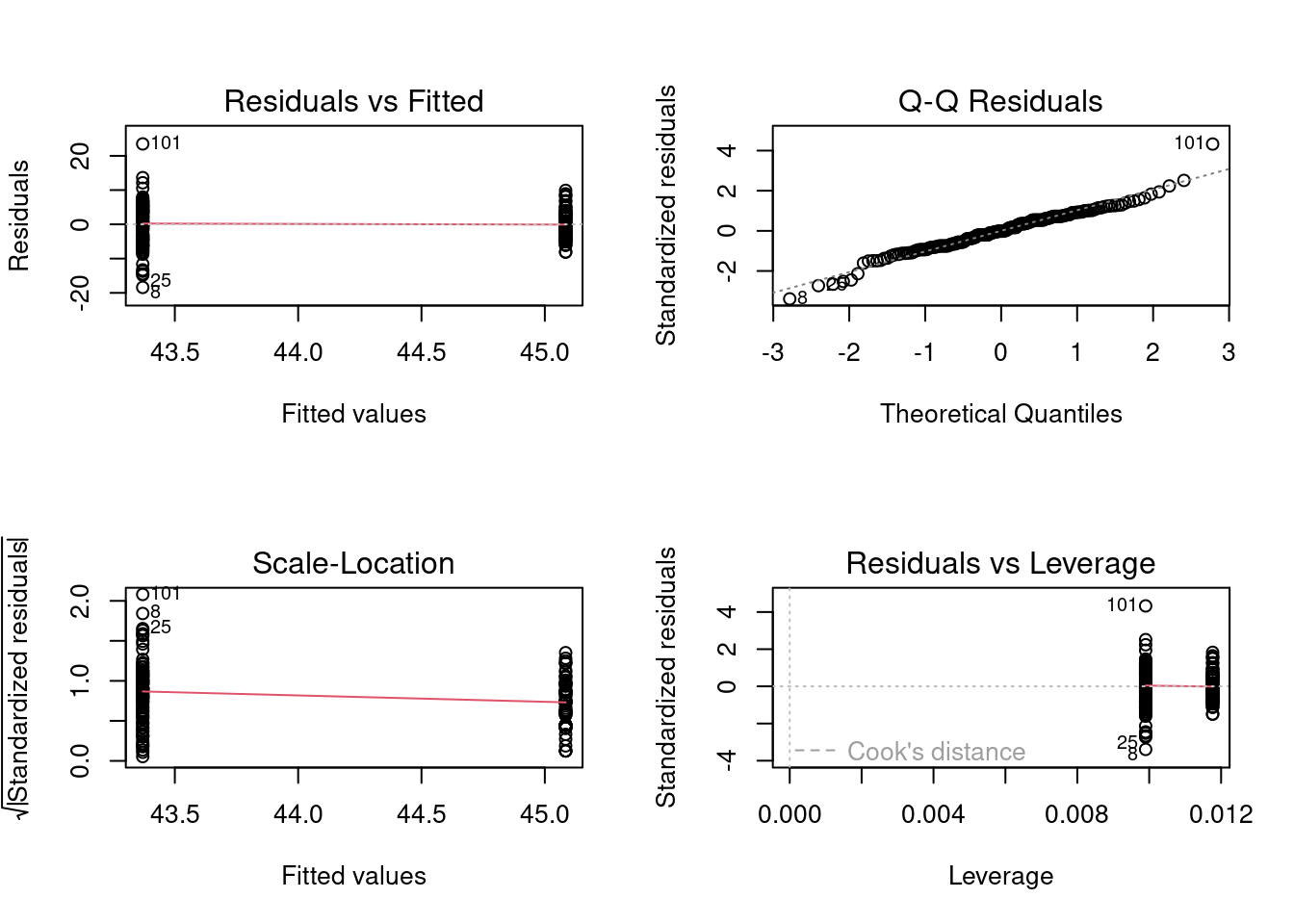
Le premier graphique ci-dessus montre comment les résidus se distribuent autour des valeurs prédites (les moyennes) pour chaque site et permet de juger si il semble y avoir un problème de normalité ou d’homoscédasticité. Si les variances étaient égales dans les deux sites, l’étendue verticale des résidus tendrait à être la même. Sur le graphique, on voit que l’étendue des résidus est plus grande à gauche (le site où la taille moyenne est la plus faible), ce qui suggère un possible problème d’homogénéité des variances. On peut tester cela plus formellement en comparant la moyenne de la valeur absolue des résidus.(on y reviendra; c’est le test de Levene).

Le deuxième graphique est un graphique de probabilité (graphique Q-Q) des résidus. Comme ici, les points tombent près de la diagonale, il ne semble pas y avoir de problème important avec la normalité. On peut faire un test formel de la condition de normalité : le test de Shapiro-Wilk:


    Shapiro-Wilk normality test

data:  residuals(m1)
W = 0.97469, p-value = 0.001857

Hummm… Ce test indique que les résidus ne sont pas normaux, ce qui contredit notre évaluation visuelle. Cependant, puisque (a) la distribution des résidus ne s’éloigne pas beaucoup de la normalité et (b) le nombre d’observations à chaque site est raisonnablement grand (i.e. >30), nul besoin d’être trop inquiet quant à l’impact de cette violation de normalité sur la fiabilité du test.

Qu’en est-il de l’égalité des variances?

Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.
Levene's Test for Homogeneity of Variance (center = median)
       Df F value    Pr(>F)    
group   1  11.514 0.0008456 ***
      184                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
bptest(m1)

    studentized Breusch-Pagan test

data:  m1
BP = 8.8015, df = 1, p-value = 0.00301

Les résultats qui précédents proviennent de 2 des tests disponibles en R (dans les package car 📦 et lmtest 📦) qui éprouvent l’hypothèse de l’égalité des variances dans des tests de t ou des modèles linéaires ayant uniquement des variables indépendantes discontinues ou catégoriques. Il est inutile de faire les 2 tests. Si ils sont présentés ici, c’est que ces 2 tests sont usuels et qu’il n’y a pas consensus quant au meilleur des deux. Le test de Levene est le plus connu et utilisé. Il compare la moyenne des valeurs absolues des résidus dans les deux groupes. Le test Breusch-Pagan a l’avantage d’être applicable à une plus large gamme de modèles linéaires (il peut être utilisé également avec des variables indépendantes continues, comme en régression). Ici, les deux tests mènent à la même conclusion: la variance diffère entre les deux sites.

Sur la base de ces résultats, on peut conclure qu’il y a des éléments (même si faibles) pour rejeter l’hypothèse nulle qu’il n’y a pas de différence dans la taille de poissons entre les deux sites. On a utilisé une modification du test de t pour tenir compte du fait que les variances ne sont pas égales et nous sommes satisfaits que la condition de normalité des résidus a été remplie. Alors, “fklngth” à Cumberland est plus grande que “fklngth” à The Pas.

10.4 Bootstrap et tests de permutation pour comparer deux moyennes

10.4.1 Bootstrap

Le bootstrap et les tests de permutation peuvent être utilisés pour comparer les moyennes (ou d’autres statistiques). Le principe général est simple et peut être effectué de diverses façons. Ici on utilise certains des outils disponibles et le fait qu’une comparaison de moyenne peut être représentée par un modèle linéaire. On pourra utiliser un programme similaire plus tard quand on ajustera des modèles plus complexes (mais plus amusants !).

library(boot)

La première section sert à définir une fonction (ici appelée bs) qui extraie les coefficients d’un modèle ajusté :

# Fonction pour extraire les coefficients d'un modèle pour chaque itérations.
bs <- function(formule, data, indices) {
  d <- data[indices, ]
  fit <- lm(formule, data = d)
  return(coef(fit))
}

La deuxième section avec la commande boot() fait le gros du travail: on prend les données dans “sturgeon”, on les bootstrap \(R = 1000\) fois, et chaque fois on ajuste le modèle fklngth vs location et on garde les valeurs calculées par la fonction bs.

# bootstrap avec 1000 réplications.
resultats <- boot(data = esturgeon, statistic = bs, R = 1000,
                formule = fklngth ~ location)
# Affichez les résultats.
resultats

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = esturgeon, statistic = bs, R = 1000, formule = fklngth ~ 
    location)


Bootstrap Statistics :
     original       bias    std. error
t1* 45.084391 -0.010974135   0.4225382
t2* -1.714546  0.004510085   0.7645004

On obtient les estimés originaux pour les deux coefficients du modèle: la moyenne pour le premier (alphabétiquement) site soit Cumberland, et la différence entre les deux moyennes à Cumberland et The Pas. C’est ce second paramètre, la différence entre les moyennes, qui nous intéresse.

plot(resultats, index = 2)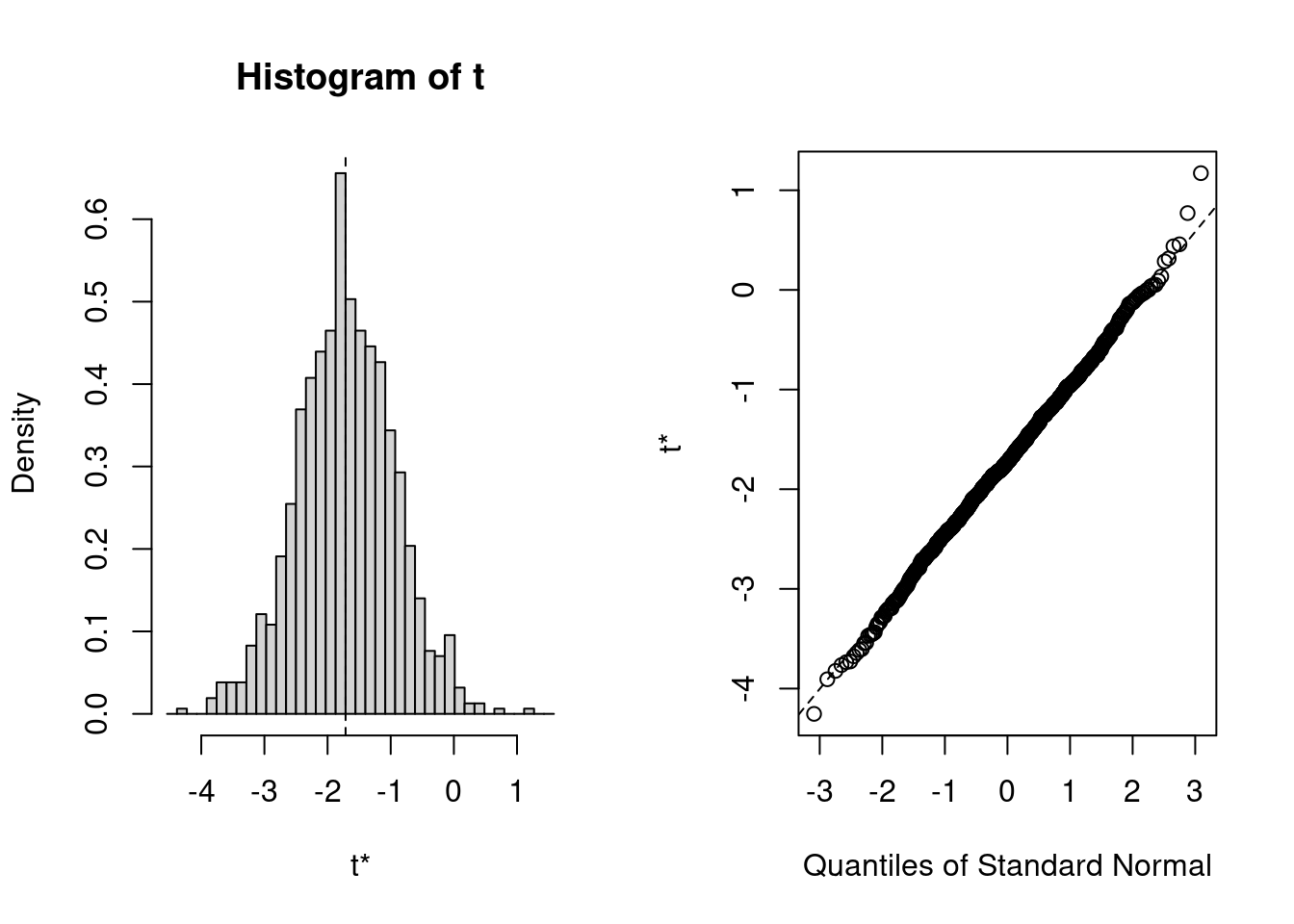
Figure 10.4: Normalité des estimés de la différence des moyennes par bootstrap. 
# Calculez l'intervalle de confiance à 95%.
boot.ci(resultats, type = "bca", index = 2)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates

CALL : 
boot.ci(boot.out = resultats, type = "bca", index = 2)

Intervals : 
Level       BCa          
95%   (-3.220, -0.129 )  
Calculations and Intervals on Original Scale

Comme l’intervalle de confiance n’inclue pas 0, on conclue que les moyennes ne sont pas les mêmes.

10.4.2 Permutation

Les tests de permutation pour les modèles linéaires peuvent être effectués à l’aide du package lmPerm 📦 :

m1Perm <- lmp(fklngth ~ location,
              data = esturgeon,
              perm = "Prob")
[1] "Settings:  unique SS "

La fonction lmp() fait tout le travail pour nous. Ici, cette fonction est effectuée avec l’option perm pour choisir la règle utilisée pour stopper les calculs. L’option “Prob” arrête les permutations quand la déviation standard estimée pour la p-valeur tombe sous un seuil déterminé. C’est l’une des nombreuses règles qui peuvent possiblement être utilisées pour ne faire les permutations que sur un sous-ensemble des permutations possibles (ce qui prendrait souvent trèèèèès longtemps).

summary(m1Perm)

Call:
lmp(formula = fklngth ~ location, data = sturgeon, perm = "Prob")

Residuals:
      Min        1Q    Median        3Q       Max 
-18.40921  -3.75370  -0.08439   3.76598  23.48055 

Coefficients:
          Estimate Iter Pr(Prob)  
location1   0.8573 3150   0.0308 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.454 on 184 degrees of freedom
Multiple R-Squared: 0.02419,    Adjusted R-squared: 0.01889 
F-statistic: 4.562 on 1 and 184 DF,  p-value: 0.03401
  1. Iter: la règle a limité le calcul à 0.4013591 permutations. Notez que ce nombre va varier à chaque fois que vous ferez tourner ce code. Ce sont des résultats obtenus par permutations aléatoires, donc vous devez vous attendre à de la variabilité. .
  2. Pr(Prob): La p-valeur estimée pour H0 est 2.1359. La différence observée pour “fklngth” entre les deux sites était plus grande que les valeurs permutées pour environ (1 - 2.1359= -113.6%) des 0.4013591 permutations. Notez que 0.4013591 permutations ce n’est pas un si grand nombre de permutations que ça, et donc les faibles valeurs de p ne sont pas très précises. Si vous voulez des valeurs précises de p, vous devrez faire plus de permutations. Vous pouvez ajuster 2 paramètres: maxIter, le nombre maximal de permutations (défaut 5000) et Ca, le seuil de précision désiré qui arrête les permutations quand l’erreur-type de p est plus petite que Ca*p (défaut=0.1)
  3. F-statistic: Le reste est la sortie standard pour un modèle ajusté à des données, avec le test paramétrique. Ici, la p-valeur, présumant que toutes les conditions d’application sont remplies, est 0.034.

10.5 Comparer les moyennes de deux échantillons appariés

Avertissement

Pour la section suivante veuillez télécharger le jeu de données skulldat_2020.csv qui a été récemment ajouté sur Brightspace.

Dans certaines expériences les mêmes individus sont mesurés deux fois, par exemple avant et après un traitement ou encore à deux moments au cours de leur développement. Les mesures obtenues lors de ces deux évènements ne sont donc pas indépendantes, et des comparaisons de ces mesures appariées doivent être faites.

Le jeu de données skulldat_2020.csv contient des mesures de la partie inférieure du visage de jeunes filles d’Amérique du Nord prises à 5 ans, puis à 6 ans (données de Newman and Meredith, 1956).

  • Pour débuter, éprouvons l’hypothèse que la largeur de la figure est la même à 5 ans et à 6 ans en assumant que les mesures viennent d’échantillons indépendants.
crane <- read.csv("data/skulldat_2020.csv")
t.test(width ~ age,
       data = crane,
       alternative = "two.sided")

    Welch Two Sample t-test

data:  width by age
t = -1.7812, df = 27.93, p-value = 0.08576
alternative hypothesis: true difference in means between group 5 and group 6 is not equal to 0
95 percent confidence interval:
 -0.43002624  0.03002624
sample estimates:
mean in group 5 mean in group 6 
       7.461333        7.661333

Jusqu’à maintenant, nous avons spécifié le test de t en utilisant une notation de type formule avec y ~ x où y est la variable pour laquelle on souhaite comparer les moyennes et x correspond à une variable définissant les groupes. Cela marche bien lorsque les données ne sont pas appariées et sont présentées dans un format de type long où les données prise dans une même catégorie ou sur une même personne sont simplement les unes en-dessous des autres avec des colonnes indiquant l’appartenance des mesures aux différentes catégories (voir la structure de crane par exemple) Dans le jeu de données crane, il y a 3 colonnes:

  • width: largeur de la tête
  • age: age lors de la mesure
  • id: identité de la personne
head(crane)
  width age id
1  7.33   5  1
2  7.53   6  1
3  7.49   5  2
4  7.70   6  2
5  7.27   5  3
6  7.46   6  3

Quand les données sont appariées, il faut indiquer comment elles doivent être associées. Dans notre exemple, elles sont appariées par individu. Le format de données de type long indique cet appariement via la colonne id. Cependant, la fonction t.test ne permet pas de le prendre en compte. Il faut donc transformer les données en format de type large ou horizontale ou il y a une colonne différente pour chaque catégorie. Dans notre exemple, on veut un jeu de données avec une colonne de mesure par age et où chaque ligne correspond à une personne différente. On peut modifier le format des données avec le code suivant.

crane_h <- data.frame(id = unique(crane$id))
crane_h$width5 <- crane$width[match(crane_h$id, crane$id) & crane$age == 5]
crane_h$width6 <- crane$width[match(crane_h$id, crane$id) & crane$age == 6]
head(crane_h)
  id width5 width6
1  1   7.33   7.53
2  2   7.49   7.70
3  3   7.27   7.46
4  4   7.93   8.21
5  5   7.56   7.81
6  6   7.81   8.01

Maintenant, effectuons le test apparié qui est approprié: Que conclure? Comment les résultats diffèrent-ils de la première analyse? Pourquoi?

t.test(crane_h$width5, crane_h$width6,
  alternative = "two.sided",
  paired = TRUE
)

    Paired t-test

data:  crane_h$width5 and crane_h$width6
t = -19.72, df = 14, p-value = 1.301e-11
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -0.2217521 -0.1782479
sample estimates:
mean difference 
           -0.2

La première analyse a comme supposition que les deux échantillons de filles de 5 et 6 ans sont indépendants, alors que la deuxième analyse a comme supposition que la même fille a été mesurée deux fois, une fois à 5 ans, et la deuxième fois à 6 ans.

Notez que, dans le premier cas, on accepte l’hypothèse nulle, mais que le test apparié rejette l’hypothèse nulle. Donc, le test qui est approprié (le test apparié) indique un effet très significatif de l’âge, mais le test inapproprié suggère que l’âge n’importe pas. C’est parce qu’il y a une très forte corrélation entre la largeur du visage à 5 et 6 ans:

graphcrane <- ggplot(data = crane_h, aes(x = width5, y = width6)) +
  geom_point() +
  labs(x = "Largeur du visage à 5 ans", y = "Largeur du visage à 6 ans") +
  geom_smooth() +
  scale_fill_continuous(low = "lavenderblush", high = "red")

graphcrane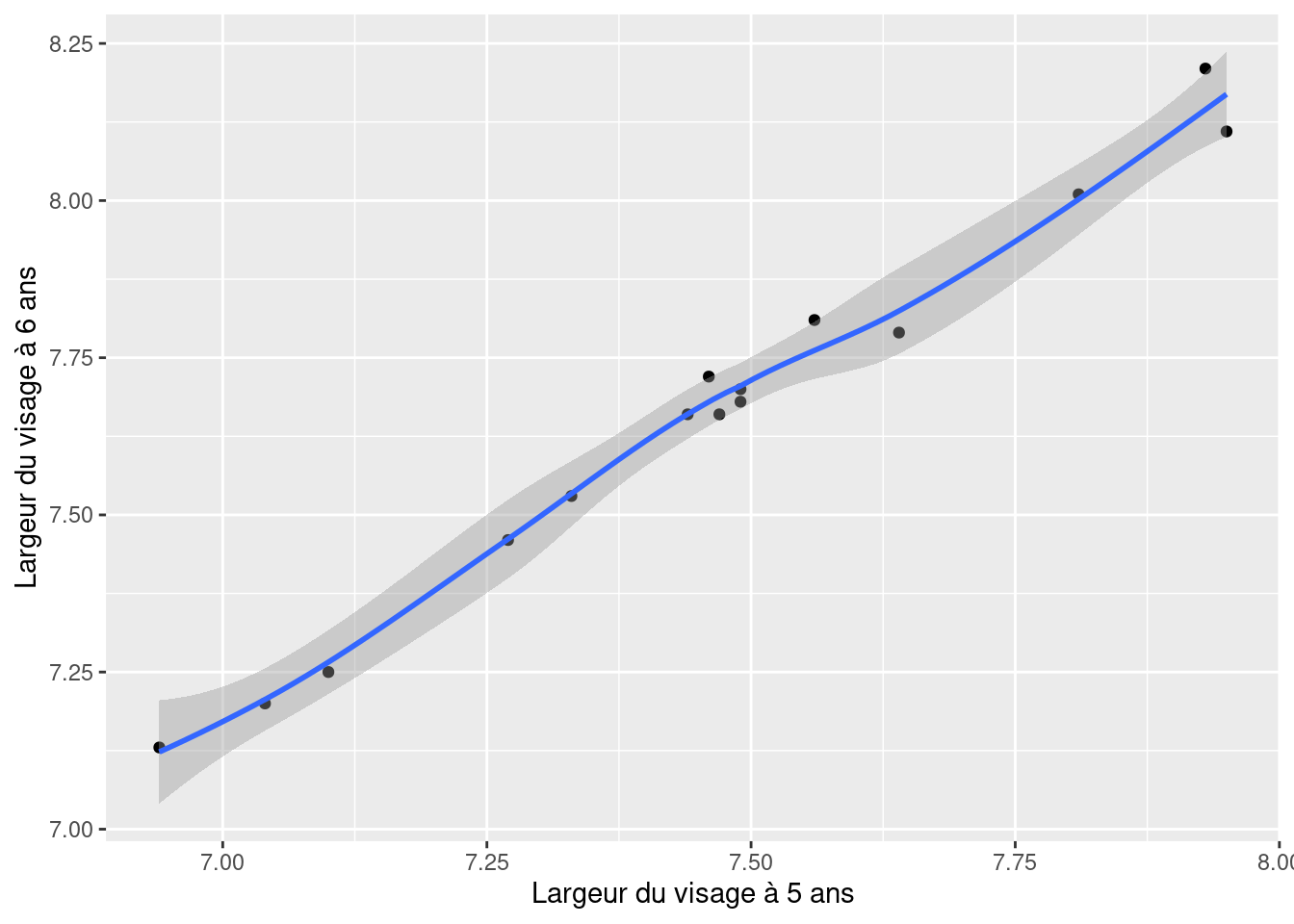
Figure 10.5: Relation entre la largeur du visage à 5 et 6 ans.

Avec r = 0.9930841. En présence d’une si forte corrélation, l’erreur-type de la différence appariée de largeur du visage entre 5 et 6 ans est beaucoup plus petite que l’erreur-type de la différence entre la largeur moyenne à 5 ans et la largeur moyenne à 6 ans. Par conséquent, la statistique t associée est beaucoup plus élevée pour le test apparié, la puissance du test est plus grande, et la valeur de p plus petite.

  • Répétez l’analyse en utilisant l’alternative non paramétrique, le test Wilcoxon rang-signés (signed-rank). (Que concluez-vous?
wilcox.test(crane_h$width5, crane_h$width6,
  alternative = "two.sided",
  paired = TRUE
)
Warning in wilcox.test.default(crane_h$width5, crane_h$width6, alternative =
"two.sided", : cannot compute exact p-value with ties

    Wilcoxon signed rank test with continuity correction

data:  crane_h$width5 and crane_h$width6
V = 0, p-value = 0.0007193
alternative hypothesis: true location shift is not equal to 0

Donc on tire la même conclusion qu’avec le test de t apparié et on conclue qu’il y a des différences significatives entre la taille des crânes de filles âgées de 5 et 6 ans (quelle surprise !).

Mais, attendez une minute ! On a utilisé des tests bilatéraux ici mais, compte tenu des connaissances sur la croissance des enfants, une hypothèse unilatérale serait préférable. Ceci peut être accommodé en modifiant l’option “alternative”. On utilise l’hypothèse alternative pour décider entre “less” ou “greater”. Ici, si il y a une différence, on s’attend à ce que width5 sera inférieur à width6, donc on utiliserait “less”.

t.test(crane_h$width5, crane_h$width6,
  alternative = "less",
  paired = TRUE
)

    Paired t-test

data:  crane_h$width5 and crane_h$width6
t = -19.72, df = 14, p-value = 6.507e-12
alternative hypothesis: true mean difference is less than 0
95 percent confidence interval:
       -Inf -0.1821371
sample estimates:
mean difference 
           -0.2 
wilcox.test(crane_h$width5, crane_h$width6,
  alternative = "less",
  paired = TRUE
)
Warning in wilcox.test.default(crane_h$width5, crane_h$width6, alternative =
"less", : cannot compute exact p-value with ties

    Wilcoxon signed rank test with continuity correction

data:  crane_h$width5 and crane_h$width6
V = 0, p-value = 0.0003597
alternative hypothesis: true location shift is less than 0

Pour estimer la puissance d’un test de t avec R, il faut utiliser la fonction pwr.t.test(). Il faut spécifier l’argument type = "paired", utiliser la moyenne et l’écart-type de la différence pour calculer le d de cohen avec la formule mean(diff) / sd(diff) pour un test de t pairé.

crane_h$diff <- crane_h$width6 - crane_h$width5
pwr.t.test(n = 15,
             d = mean(crane_h$diff) / sd(crane_h$diff),
             type = "paired")

     Paired t test power calculation 

              n = 15
              d = 5.091751
      sig.level = 0.05
          power = 1
    alternative = two.sided

NOTE: n is number of *pairs*

10.6 Références

Bumpus, H.C. (1898) The elimination of the unfit as illustrated by the introduced sparrow, Passer domesticus. Biological Lectures, Woods Hole Biology Laboratory, Woods Hole, 11 th Lecture: 209 - 226.

Newman, K.J. and H.V. Meredith. (1956) Individual growth in skele- tal bigonial diameter during the childhood period from 5 to 11 years of age. Amer. J. Anat. 99: 157 - 187.