Introduction Bayesian statistics

Why make it simple when you could go Bayesian

Julien Martin

BIO 8940 - Lecture 7

2024-09-19

Overview …

• For many years – until recently – Bayesian ideas in statistics were widely dismissed, often without much thought
• Advocates of Bayes had to fight hard to be heard, leading to an ‘us against the world’ mentality – & predictable backlash
• Today, debates tend be less acrimonious, and more tolerant

Bayes’ Theorem

Formal

Bayes’ theorem is the results in a conditional probability of two events:

\[ P[A|B] = \frac{P[A\ \&\ B]}{P[B]} = \frac{P[B|A] P[A]}{P[B]} \]

The conditional probability of A given B is the conditional probability ob B given A scaled by the relative probability of A compared to B.

\[ \underbrace{P[A|B]}_\text{posterior probability} = \frac{\overbrace{P[B|A]}^\text{likelihood} \cdot \overbrace{P[A]}^\text{prior probability}}{\underbrace{P[B]}_\text{marginal probability}} \]

Reframed for hypothesis

Bayes’ theorem can be seen as the conditonal probability of a hypothesis given the data: \[ P[H_0 | \text{data}] = \frac{\overbrace{P[\text{data}|H_0]}^\text{likelihood} \cdot \overbrace{P[H_0]}^\text{prior}}{P[data]} \]

Or it can be seen as \[ \underbrace{P[H_0 | \text{data}]}_{\text{what we want to know}} = \frac{\overbrace{P[\text{data}|H_0]}^\text{what frequentist do} \cdot \overbrace{P[H_0]}^\text{what we have a hard time understanding}}{\underbrace{P[data]}_\text{what we happily ignore}} \]

Bayesian inference

Error type and false positive/negative

Here we are counting number of observations in each case

Reality	Reject H0	Accept H0	Total
H0 is true	a (Type I error)	b	a + b
H0 is false	c	d (type II error)	c + d
Total	a+c	b+d	N (number of obs)

False positive \(P[H_0 \text{ true} | \text{Reject }H_0] = \frac{a}{a+c}\)

False negative: \(P[H_0\ false | Accept\ H_0] = \frac{d}{b+d}\)

Error type and false positive/negative

Same thing but with probabilities instead of number of observations

Reality	Reject H0 \([\not H_0]\)	Accept H0 \([H_0]\)	Total
H0 true [H0+]	\(P[H_0^+| \not H_0] P[H_0^+]\)	\(P[H_0^+| H_0] P[H_0^+]\)	\(P[H_0^+]\)
H0 false [H0-]	\(P[H_0^-| \not H_0] P[H_0^-]\)	\(P[H_0^-| H_0] P[H_0^-]\)	\(P[H_0^-]\)
Total	\(P[\not H_0]\)	\(P[H_0]\)	1

False positive \(P[H_0 \text{ true} | \text{Reject }H_0]\) \[ \begin{align} P[H_0^+ | \not H_0] &=\frac{P[\not H_0 | H_0^+ ] P[H_0^+ ]}{P[\not H_0]} \\ &= \frac{P[\not H_0 | H_0^+ ] P[H_0^+]} {P[\not H_0 | H_0^+] P[H_0^+ ] + P[ \not H_0 | H_0^- ] P[H_0^-]} \end{align} \]

Applied to Covid

Why does it matter? If 1% of a population have covid, for a screening test with 80% sensitivity (1- Type II) and 95% specificity (1-Type I).

Assuming N test = 100,

Reality	Test +ve	Test -ve	Total
Healthy
Has COVID
Total			100

Applied to Covid

Why does it matter? If 1% of a population have covid, for a screening test with 80% sensitivity (1- Type II) and 95% specificity (1-Type I).

Assuming N test = 100

Reality	Test +ve	Test -ve	Total
Healthy			99
Has COVID			1
Total			100

1. Adding the prior

Applied to Covid

Why does it matter? If 1% of a population have covid, for a screening test with 80% sensitivity (1- Type II) and 95% specificity (1-Type I).

Assuming N test = 100

Reality	Test +ve	Test -ve	Total
Healthy			99
Has COVID	0.8	0.2	1
Total			100

1. Adding the prior
2. Adding the Type II error

Applied to Covid

Why does it matter? If 1% of a population have covid, for a screening test with 80% sensitivity (1- Type II) and 95% specificity (1-Type I).

Assuming N test = 100

Reality	Test +ve	Test -ve	Total
Healthy	4.95	94.05	99
Has COVID	0.8	0.2	1
Total			100

1. Adding the prior
2. Adding the Type II error
3. Adding the Type I error

Applied to Covid

Why does it matter? If 1% of a population have covid, for a screening test with 80% sensitivity (1- Type II) and 95% specificity (1-Type I).

Assuming N test = 100

Reality	Test +ve	Test -ve	Total
Healthy	4.95	94.05	99
Has COVID	0.8	0.2	1
Total	5.75	94.25	100

1. Adding the prior
2. Adding the Type II error
3. Adding the Type I error
4. Adding colum sums

Applied to Covid

Why does it matter? If 1% of a population have covid, for a screening test with 80% sensitivity (1- Type II) and 95% specificity (1-Type I).

Reality	Test +ve	Test -ve	Total
Healthy	4.95	94.05	99
Has COVID	0.8	0.2	1
Total	5.75	94.25	100

• True positive: P[ Covid | test + ] = 0.139
• True negative: P[ Healthy | test - ] = 0.998
• False positive: P[ Healthy | test + ] = 0.861
• False negative: P[ Covid | test - ] = 0.002

Talk about changing prior implications

What if COVID % changes?

Why does it matter? If 20% of a population have covid instead of 1%?

Reality	Test +ve	Test -ve	Total
Healthy	4	76	80
Has COVID	16	4	20
Total	20	80	100

• True positive: P[ Covid | test + ] = 0.8
• True negative: P[ Healthy | test - ] = 0.95
• False positive: P[ Healthy | test + ] = 0.2
• False negative: P[ Covid | test - ] = 0.05

Explain impact of changing prior on test results reliability

Prosecutor’s fallacy

Mixing up P[ A | B ] with P[ B | A ] is the Prosecutor’s Fallacy

small P evidence given innocence \(\neq\) small P of innocence given evidence

True Story

• After the sudden death of two baby sons, Sally Clark was sentenced to life in prison in 1999
• Expert witness Prof Roy Meadow had interpreted the small probability of two cot deaths as a small probability of Clark’s innocence
• After a long campaign, including refutation of Meadow’s statistics (among other errors), Clark was cleared in 2003
• After being freed, she developed alcoholism and died in 2007

Meeting mosquitoes

Bayes’ Theorem

Bayes’ Theorem is a rule about the ‘language’ of probabilities, that can be used in any analysis describing random variables, i.e. any data analysis.

Q. So why all the fuss?

A. Bayesian inference uses more than just Bayes’ Theorem

Bayesian inference uses the ‘language’ of probability to describe what is known about parameters.

Warning

Frequentist inference, e.g. using p-values & confidence intervals, does not quantify what is known about parameters. many people initially think it does; an important job for instructors of intro Stat/Biostat courses is convincing those people that they are wrong

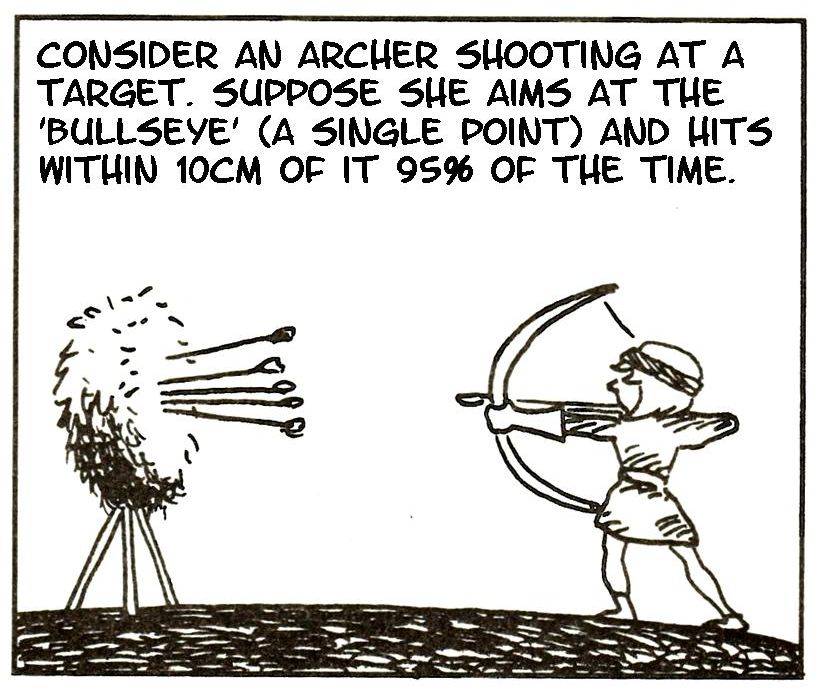
Frequentist and Bayesian

A shooting cartoon

Adapted from Gonick & Smith, The Cartoon Guide to Statistics

We ‘trap’ the truth with 95% confidence. 95% of what?

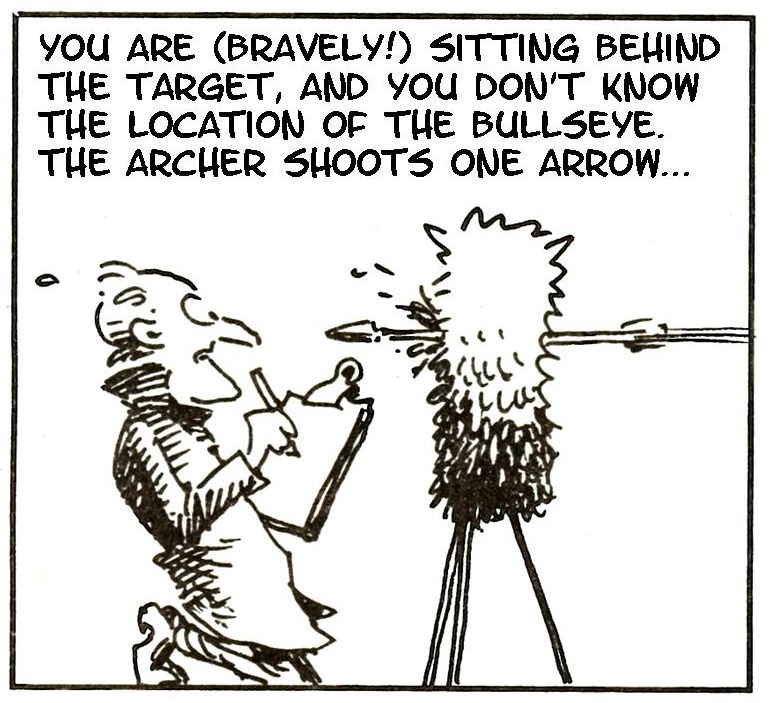
95% of what?

• We ‘trap’ the truth with 95% confidence.
• 95% of what?
• The interval traps the truth in 95% of experiments.

To define anything frequentist, you have to imagine repeated experiments.

Let’s do some more ‘target practice’, for frequentist testing

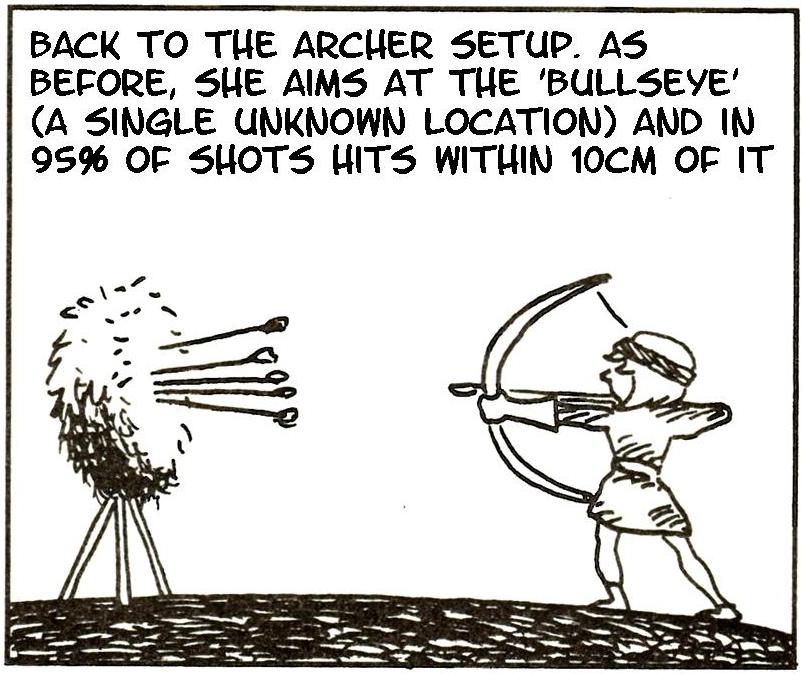
Frequentist testing

• imagine running your experiment again and again, so
  • On day 1 you collect data and construct a [valid] 95% confidence interval for a parameter \(\theta_1\).
  • On day 2 you collect new data and construct a 95% confidence interval for an unrelated parameter \(\theta_2\).
  • On day 3 … [the same]. and so on constructing confidence intervals each time
• … 95% of your intervals will trap the true parameter value

• … it does not says anything about whether your data is in the 95% or the 5%
• … it requires you to think about many other datasets, not just the one you have to analyze

How does Bayesian inference differ? Let’s take aim…

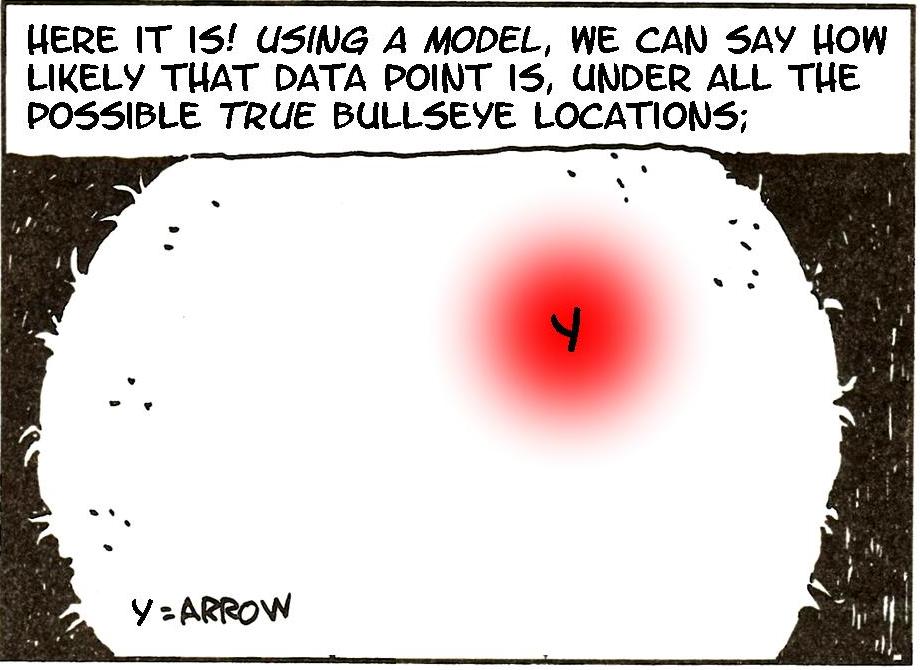
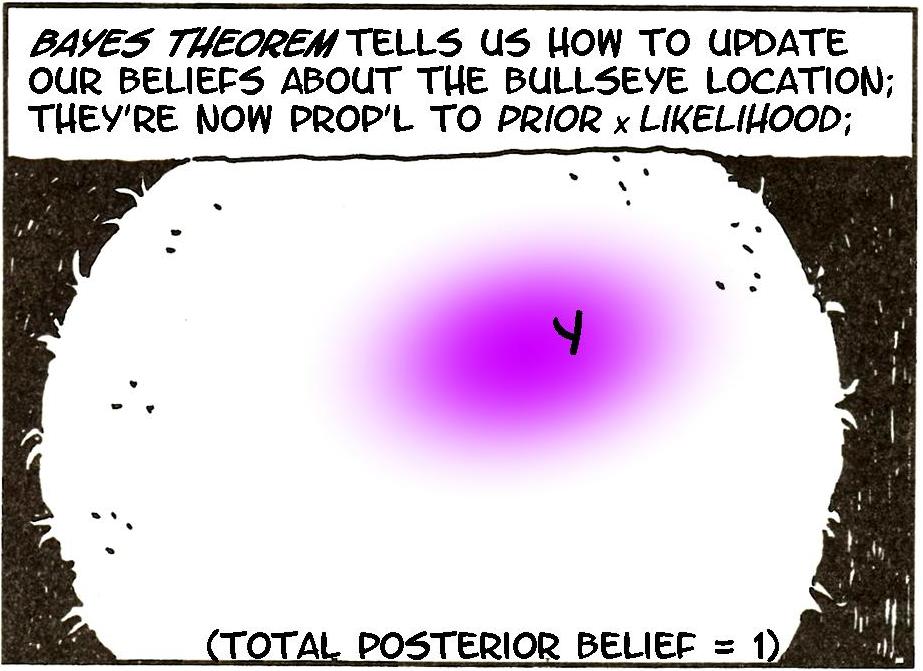
Here it is in practice

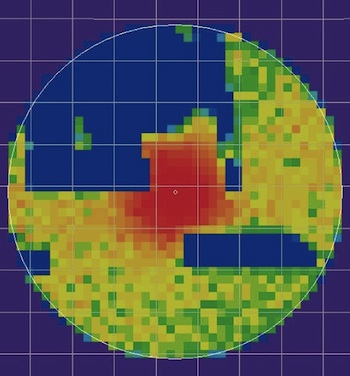
• Air France Flight 447 crashed in the ocean On June 1, 2009.

• Major wreckage recovered within 5 days. No blackbox

• Probability of blackbox location described via Bayesian inference

• Eventually, the black box was found in the red area

Bayesian inference

Updating knowledge

We use:

• Prior distribution: what you know about parameter β, excluding the information in the data – denoted \(P_{prior}(β)\)
• Likelihood: based on modeling assumptions, how [relatively] likely the data Y are if the truth is β - denoted \(f(Y|β)\)

To get a posterior distribution, denoted \(P_{post}(β|Y)\): stating what we know about β combining the prior with the data – ?

Bayes Theorem used for inference tells us:

\[ \begin{align} P_{post}(β|Y) &∝ f(Y|β) × P_{prior}(β)\\ \text{Posterior} &∝ \text{Likelihood} × \text{Prior} \end{align} \]

… and that’s it! (essentially!)

• No replications – e.g. no replicate plane searches
• Given modeling assumptions & prior, process is automatic
• Keep adding data, and updating knowledge, as data becomes available… knowledge will concentrate around true β

Updating knowledge

Updating knowledge

Updating knowledge

Updating knowledge

A Bayesian is one who, vaguely expecting a horse, and catching a glimpse of a donkey, strongly believes he has seen a mule

Where do priors come from

Priors come from all data external to the current study (i.e. everything else) ‘Boiling down’ what subject-matter experts know/think is known as eliciting a prior. It’s not easy but here are some simple tips

• Discuss parameters experts understand – e.g. code variables so intercept is mean outcome in people with average covariates, not with age = height = … = 0
• Avoid leading questions (just as in survey design)
• The ‘language’ of probability is unfamiliar, help users express their uncertainty

Where do priors come from

Use stickers or a survey in the hallway

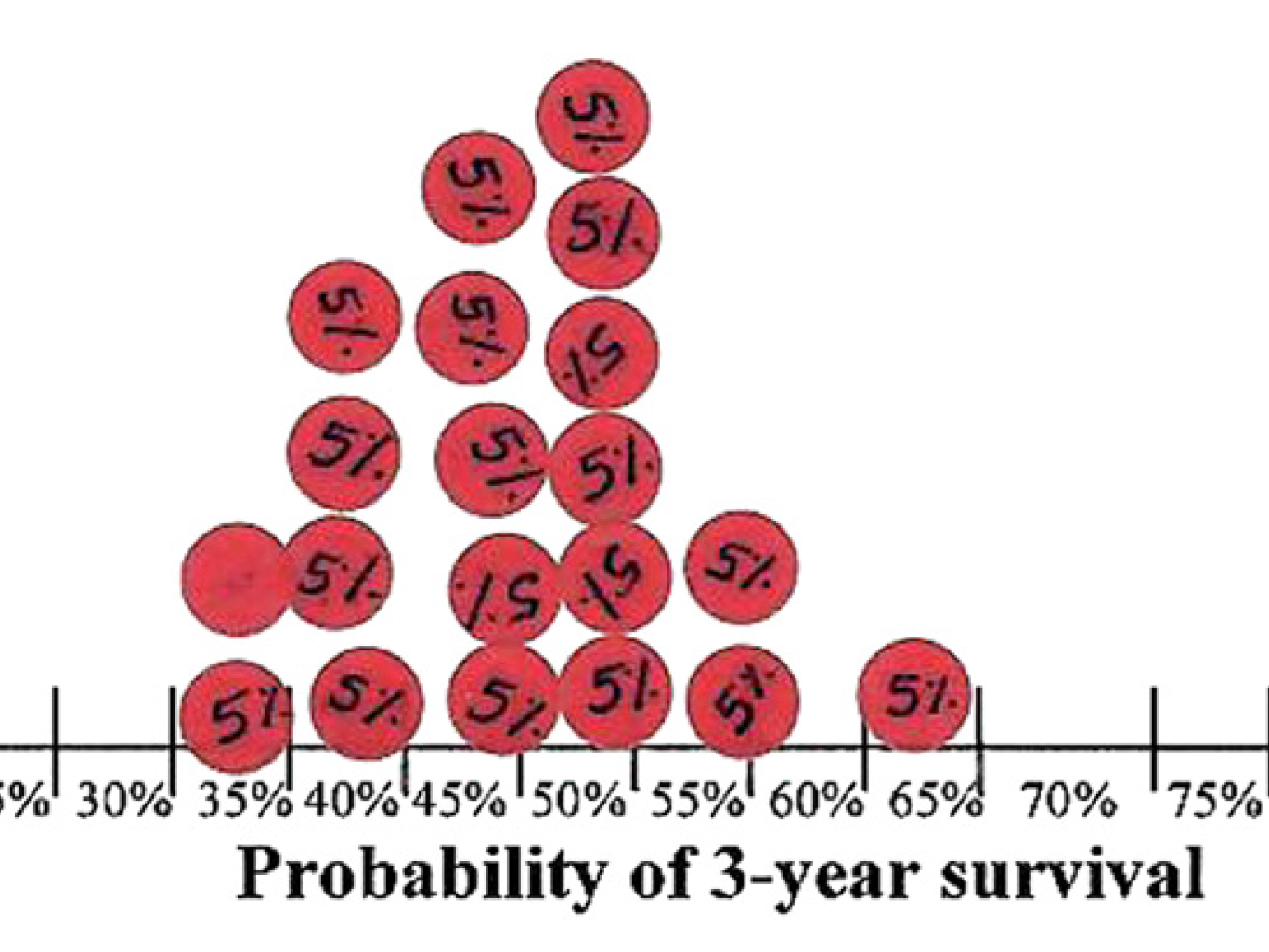
Use stickers (Johnson et al 2010, J Clin Epi) for survival when taking warfarin

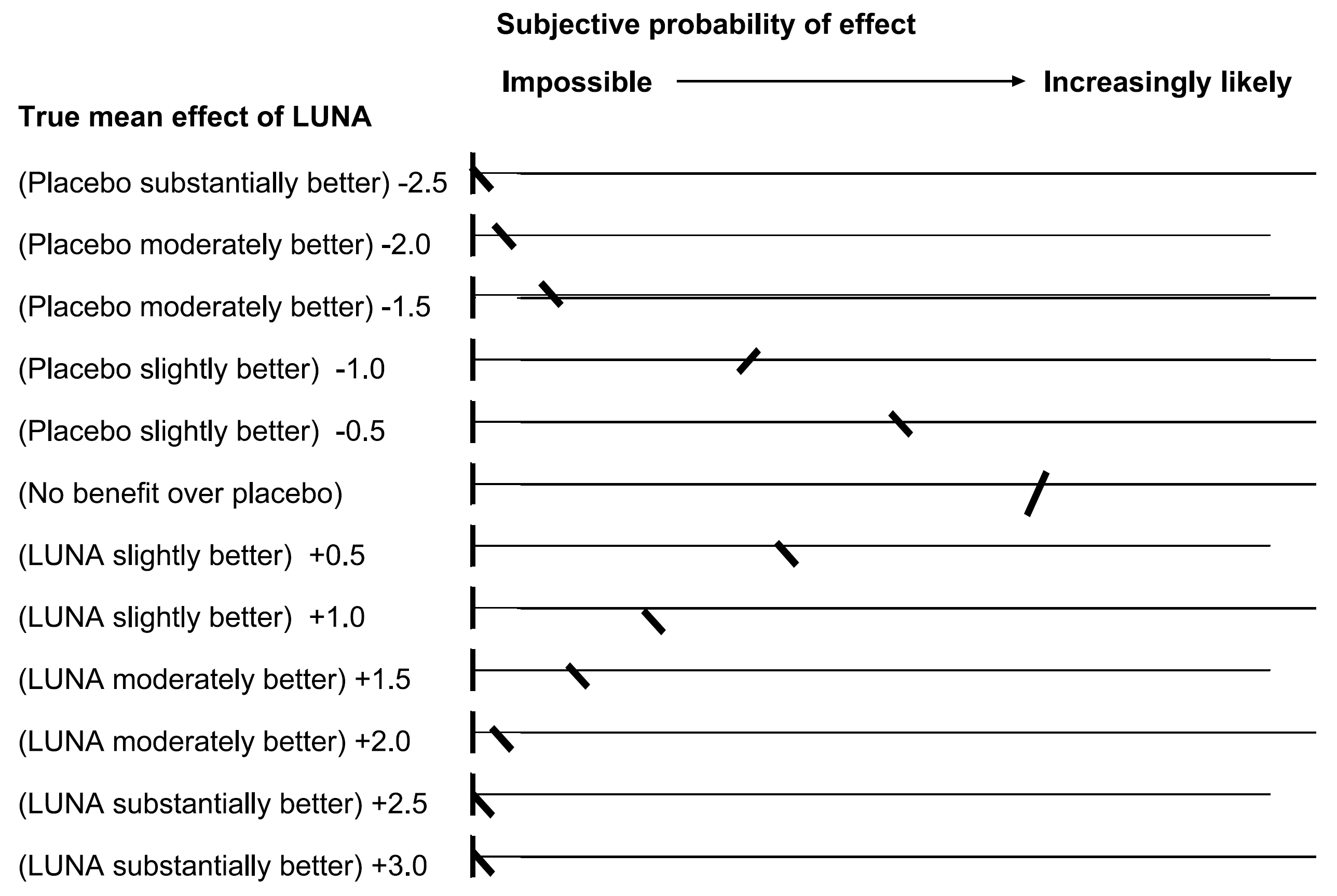
Normalize marks (Latthe et al 2005, J Obs Gync) for pain effect of LUNA vs placebo

• Ideas to help experts ‘translate’ to the language of probability
• Typically these ‘coarse’ priors are smoothed. Providing the basic shape remains, exactly how much you smooth is unlikely to be critical in practice.
• Elicitation is also very useful for non-Bayesian analyses – it’s similar to study design & analysis planning

Where do priors come from

If the experts disagree? Try it both ways

If the posteriors differ, what you believe based on the data depends on your prior knowledge

To convince other people, expect to have to convince skeptics – and note that convincing [rational] skeptics is what science is all about

When priors don’t matter (much)?

Very informative data

When the data provide a lot more information than the prior

Priors here are dominated by the likelihood, and they give very similar posteriors – i.e. everyone agrees. (Phew!)

Flat priors

Using very flat priors to represent ignorance

Flat priors do NOT actually represent ignorance!

Most of their support is for very extreme parameter values

Bayesian \(\approx\) frequentist

Likelihood gives the classic 95% confidence interval can be good approx of Bayesian 95% Highest Posterior Density interval

Bayesian \(\approx\) frequentist

With large samples (and some regularity conditions)

• (sane) frequentist confidence intervals and (sane) Bayesian credible intervals are essentially identical

• it’s actually okay to give Bayesian interpretations to 95% CIs, i.e. to say we have \(\neq\) 95% posterior belief that the true β lies within that range

Frequentist 😃 & Bayesian 😕

Prior strongly supporting small effects, and with data from an imprecise study

Frequentist ‘Textbook’ analysis says ‘reject’ (p < 0.05, woohoo, Nature her we go)

Bayesian Posterior is ‘shrunk’ toward zero. We’re sure true β is very small (& hard to replicate) & we’re unsure of its sign. Wait a second, about that front page

Where is Bayesian approach used

• Almost any analysis

• Bayesian arguments are often seen in

  • Hierarchical modeling (Some expert calls the classic frequentist version a “statistical no-man’s land”)

  • Complex models: for messy data, measurement error, multiple sources of data fitting them is possible under Bayesian approaches, but perhaps still not easy

Summary

Bayesian statistics:

• I barely scratched the surface

• Is useful in many settings, and you should know about it

• Is often not very different in practice from frequentist statistics. It is often helpful to think about analyses from both Bayesian and non-Bayesian points of view

• Is not reserved for hard-core mathematicians, or computer scientists, or philosophers. If you find it helpful, use it.

Happy modelling